题目内容
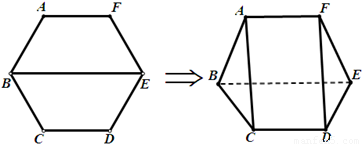
如图，把边长为2的正六边形ABCDEF沿对角线BE折起，使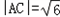
．
（1）求证：面ABEF⊥面BCDE；
（2）求五面体ABCDEF的体积．
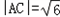．（1）求证：面ABEF⊥面BCDE；
（2）求五面体ABCDEF的体积．
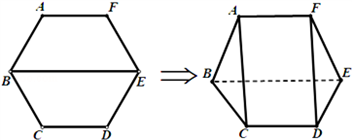
解：（1）设原正六边形中，AC∩BE=O，DF∩BE=O'，
由正六边形的几何性质可知 ，AC⊥BE，DF⊥BE
∵
，
∴OA⊥面BCDE，
∴面ABEF⊥面BCDE；
（2）由BE⊥面AOC，BE⊥面FO'D知，
面AOC∥面FO'D，
故AOC﹣FO'D是侧棱长（高）为2的直三棱柱，
且三棱锥B﹣AOC和E﹣FO'D为大小相同的三棱锥
∴VABCDEF=2VB﹣AOC+VAOC﹣FO'D
=
=
由正六边形的几何性质可知 ，AC⊥BE，DF⊥BE
∵
，∴OA⊥面BCDE，
∴面ABEF⊥面BCDE；
（2）由BE⊥面AOC，BE⊥面FO'D知，
面AOC∥面FO'D，
故AOC﹣FO'D是侧棱长（高）为2的直三棱柱，
且三棱锥B﹣AOC和E﹣FO'D为大小相同的三棱锥
∴VABCDEF=2VB﹣AOC+VAOC﹣FO'D
=
=
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
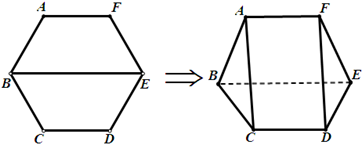（2012•江西模拟）如图，把边长为2的正六边形ABCDEF沿对角线BE折起，使
如图，把边长为2的正六边形ABCDEF沿对角线BE折起，使
．
．
．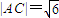