题目内容
如图1-3-14,已知∠ACB=∠ADE,∠ABC=∠AED,求证:∠ABE=∠ACD.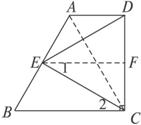
图1-3-14
思路分析:∠ABE和∠ACD分别位于△ABE和△ACD中,显然不可以利用全等来证明这两个角相等,但这两个角所在的两个三角形能相似吗?从已知条件中给的四个角分别在△ABC和△AED中,由它们相等不难证明△ABC∽△AED,这一对三角形的相似,沟通了我们想要证明的两个三角形的关系,沟通了两个角的关系.这里使用了“两边对应成比例且夹角相等,两三角形相似”的判定方法.
证明:∵∠ABC=∠AED,∠ACB=∠ADE,∴△ABC∽△AED.
∴![]() ,∠BAC=∠EAD.∴
,∠BAC=∠EAD.∴![]() .
.
∴∠BAC-∠EAC=∠EAD-∠EAC,即∠BAE=∠CAD.
∴△ABE∽△ACD.(两边对应成比例且夹角相等,两三角形相似)
∴∠ABE=∠ACD.

练习册系列答案
相关题目
 (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.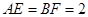 ,
,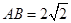 ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使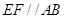 且
且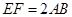 ,得一简单组合体
,得一简单组合体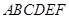 如图2示,已知
如图2示,已知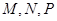 分别为
分别为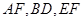 的中点.
的中点.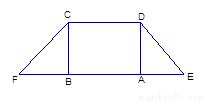
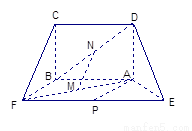
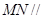 平面
平面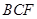 ;
;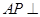
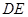 ;
; 多长时,平面
多长时,平面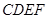 与平面
与平面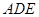 所成的锐二面角为
所成的锐二面角为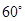 ?
?