题目内容
在 中,若
中,若 ,且
,且 (1)求角
(1)求角 的大小;
的大小;
(2)求 的面积
的面积 .
.
解:(1)由题可知:在DABC中,÷ ÷ = 2
÷ = 2 ,
,
 ×cosC +
×cosC +  ×cosA =
×cosA =  ×sinB,
×sinB,
因为:  =
=  +
+  ,
, ×cosC +
×cosC +  ×cosA = (
×cosA = ( +
+ )×sinB,
)×sinB,
即:(cosC - sinB) + (cosA - sinB)
+ (cosA - sinB) =
=  -------2分
-------2分
而 、
、 是两不共线向量,所以:
是两不共线向量,所以: Þ cosC = cosA,
Þ cosC = cosA,
0 < A,C < p , \ A = C , DABC 为等腰三角形.在等腰DABC中,A + B + C = p , \ 2A + B = p , A =  -
-  ;由上知:cosA = cos(
;由上知:cosA = cos(  -
-  )= sin
)= sin = sinB, \sin
= sinB, \sin = 2sin
= 2sin cos
cos , \ cos
, \ cos  =
= 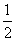 , 0 <
, 0 <  <
<  ,
,
\  =
=  , B =
, B =  ,-------------6分
,-------------6分
(2)由(1)知:则A = C =  , 由正弦定理得:
, 由正弦定理得: =
=  ,
,
\÷ ÷ = 2 , SDABC =
÷ = 2 , SDABC = 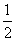 ÷
÷ ÷×÷
÷×÷ ÷sin
÷sin =
= 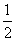 ×2
×2 ×2 ×
×2 ×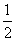 =
=  --12分
--12分

练习册系列答案
相关题目

 的取值范围是( )
的取值范围是( ) ,若函数
,若函数 有四个零点,则实数
有四个零点,则实数 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.

 设函数
设函数 且函数
且函数 的零点均在区间
的零点均在区间 内,则
内,则 的最小值为( )
的最小值为( )



 的直径
的直径 的延长线与弦
的延长线与弦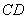 的延长线相交于点
的延长线相交于点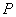 ,
,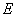 为⊙
为⊙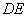 交
交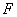 ,且
,且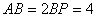 ,
,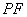 的长度.
的长度.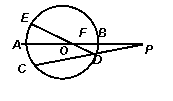
 与
与 轴以及直线
轴以及直线 所围图形的面积为( )
所围图形的面积为( ) B.
B. C.
C. D.
D.
 的定义域为
的定义域为  (B)
(B) (C)
(C) (D)
(D)
 中,以原点
中,以原点 为极点,
为极点,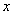 轴的正半轴为极轴,建立极坐标系.
轴的正半轴为极轴,建立极坐标系. (
( 为参数),
为参数), (
( 为参数).
为参数). ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线; 对应的参数为
对应的参数为 ,
, 为
为 中点
中点 到直线
到直线 距离的最小值.
距离的最小值.