Question

（坐标系与参数方程选做题）
在直角坐标xOy中，曲线C₁的参数方程为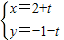（t为参数），曲线C₂的参数方程为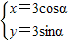（α为参数），则曲线C₁与C₂的交点个数为    ．

Answer 1

【答案】分析：求出曲线C₁的直角坐标方程为x+y-1=0，表示一条直线； 求出曲线C₂的直角坐标方程为 x²+y²=9，表示以原点O为圆心，半径为3的圆．求得圆心到直线的距离小于半径，可得直线和圆相交，从而得出结论．
解答：解：由于曲线C₁的参数方程为（t为参数），故它的直角坐标方程为x+y-1=0．
由于曲线C₂的参数方程为（α为参数），则它的直角坐标方程为 x²+y²=9，表示以原点O为圆心，半径为3的圆．
圆心到直线的距离为 d==，小于半径，故直线和圆相交，故曲线C₁与C₂的交点个数为2，
故答案为 2．
点评：本题主要考查把参数方程化为直角坐标方程，直线和圆的位置关系的判定方法，点到直线的距离公式的应用，属于基础题．