Question

（2009•宜春一模）四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PA⊥平面ABCD，且PA=2，点E是线段PD上的动点．
（1）当点E是PD的中点时，求二面角E-AC-D的大小；
（2）在（1）的条件下，求点D到平面EAC的距离；
（3）若点F是BC的中点且PF∥平面EAC时，求点E的位置．

Answer 1

分析：（1）取AD的中点O，连接E，O，则EO∥PA，可得EO⊥面ABCD．　过点O作OH⊥AC交AC于H点，连接EH，利用三垂线定理可得EH⊥AC，
从而∠EHO为二面角E-AC-D的平面角．分别求出OE和OH即可．
（2）由（1）知：AC⊥平面EOH，于是平面EOH⊥平面EAC，过点O作OG⊥EH，垂足为G，
则OG⊥平面EAC，在△EOH中，可求出OG．由于点O是线段AD的中点，因此点O到平面EAC的距离OG是点D到平面EAC 距离的一半，即可．
（3）连接FD交AC于点S，PF∥平面EAC，利用线面平行的性质定理可得PF∥ES，由F为BC中点，可得

FS

SD

=

FC

AD

=

1

2

，于是得到

PE

ED

=

FS

SD

=

1

2

．进而得出点E的位置．

解答：解：（1）取AD的中点O，连接E，O，则EO∥PA，∴EO⊥面ABCD．
　过点O作OH⊥AC交AC于H点，连接EH，则EH⊥AC，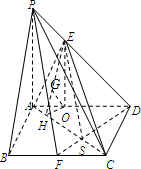
从而∠EHO为二面角E-AC-D的平面角．
在△PAD中，EO=

1

2

AP=1，在△AHO中∠HAO=45°，
∴HO=AOsin45°=

2

2

，
∴tan∠EHO=

EO

HO

=

2

，
∴二面角E-AC-D等于arctan

2

．
（2）由（1）知：AC⊥OH，AC⊥EH，因此AC⊥平面EOH，
∴平面EOH⊥平面EAC，过点O作OG⊥EH，垂足为G，
则OG⊥平面EAC，在△EOH中，易求：OG=

3

3

．
又∵点O是线段AD的中点，因此点O到平面EAC的距离OG是点D到平面EAC 距离的一半，
即点D到平面EAC距离为

2 3

3

．
（3）连接FD交AC于点S，PF∥平面EAC，平面EAC∩平面PFD=ES，
∴PF∥ES  ①
又∵F为BC中点，∴

FS

SD

=

FC

AD

=

1

2

②
由①②知：

PE

ED

=

FS

SD

=

1

2

．
即：当F是BC的中点且PF∥平面EAC时，有

PE

=

1

3

PD

．

点评：熟练掌握线面、面面垂直的判定与性质定理、二面角的定义、三垂线定理、定点平面的距离的求法、线面平行的性质定理、平行线分线段成比例定理等是解题的关键．