题目内容
将数列{an}的各项排成如图所示的三角形形状.
(1)若数列{an}是首项为1,公差为2的等差数列,写出图中第5行第5个数;
(2)若函数f(x)=a1x+a2x2+a3x3+…+anxn,且f(1)= n2,求数列{an}的通项公式;
(3)设Tm为第m行所有项的和,在(2)的条件下,用含m的代数式表示Tm.
解:(1)第5行第5个数是29.
(2)由f(1)=n2,得a1+a2+a3+…+an=n2.
设Sn是数列{an}的前n项和,∴Sn=n2.当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.
又当n=1时,2n-1=1=a1,∴an=2n-1,
即数列{an}的通项公式是an=2n-1(n=1,2,3,…).
(3)由(2)知数列{an}是首项为1,公差为2的等差数列.
∵前m-1行共有项1+2+3+…+(m-1)=![]() ×(m-1)=
×(m-1)=![]() ,
,
∴第m行的第一项为![]() +1=2×(
+1=2×(![]() +1)-1=m2-m+1.
+1)-1=m2-m+1.
∴第m行构成首项为m2-m+1,公差为2的等差数列,且有m项.
∴Tm=(m2-m+1)×m+![]() ×2=m3.
×2=m3.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 将数列{an}的各项排成如图所示的三角形形状.
将数列{an}的各项排成如图所示的三角形形状.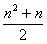 ,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.
,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.

