题目内容
设P为函数f(x)=sin(πx)的图象上的一个最高点,Q为函数g(x)=cos(πx)的图象上的一个最低点,则|PQ|最小值是
- A.

- B.2
- C.
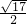
- D.2

C
分析:分别令f(x)=1,g(x)=-1,可求得P、Q点的坐标,再用两点间距离公式可把|PQ|表示出来,由二次函数的性质可求得其最小值.
解答:令f(x)=sin(πx)=1,则πx= ,解得x=
,解得x= +2k1,k1∈Z,
+2k1,k1∈Z,
所以P( +2k1,1),
+2k1,1),
令g(x)=cos(πx)=-1,则πx=π+2k2π,解得x=1+2k2,k2∈Z,
所以Q(1+2k2,-1),
所以|PQ|= =
= ,
,
因为k1,k2∈Z,所以k1-k2∈Z,
所以当k1=k2时,|PQ|取得最小值为 ,
,
故选C.
点评:本题考查正、余弦函数的图象、两点间距离公式,考查数形结合思想,属中档题.
分析:分别令f(x)=1,g(x)=-1,可求得P、Q点的坐标,再用两点间距离公式可把|PQ|表示出来,由二次函数的性质可求得其最小值.
解答:令f(x)=sin(πx)=1,则πx=
 ,解得x=
,解得x= +2k1,k1∈Z,
+2k1,k1∈Z,所以P(
 +2k1,1),
+2k1,1),令g(x)=cos(πx)=-1,则πx=π+2k2π,解得x=1+2k2,k2∈Z,
所以Q(1+2k2,-1),
所以|PQ|=
 =
= ,
,因为k1,k2∈Z,所以k1-k2∈Z,
所以当k1=k2时,|PQ|取得最小值为
 ,
,故选C.
点评:本题考查正、余弦函数的图象、两点间距离公式,考查数形结合思想,属中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 的图象上的一个最高点,Q为函数g(x)=
的图象上的一个最高点,Q为函数g(x)= 图象上的一个最低点,则|PQ|的最小值为( )
图象上的一个最低点,则|PQ|的最小值为( )


