题目内容
设函数f是定义在正整数有序对集合上的函数,并满足:①f(x,x)=x,②f(x,y)=f(y.x)③(x+y)f(x,y)=yf(x,x+y),则f(12,16)+f(16,12)的值是( )A.96
B.64
C.48
D.24
【答案】分析:由函数性质的第3条,可得f(x,x+y)= f(x,y),从而得到f(12,16)=4f(12,12)=4×12=48,再结合f(x,y)=f(y,x)得f(16,12)=f(12,16)=48,从而得到f(12,16)+f(16,12)的值.
f(x,y),从而得到f(12,16)=4f(12,12)=4×12=48,再结合f(x,y)=f(y,x)得f(16,12)=f(12,16)=48,从而得到f(12,16)+f(16,12)的值.
解答:解:∵(x+y)f(x,y)=yf(x,x+y),
∴f(x,x+y)=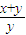 f(x,y),
f(x,y),
因此,f(12,16)=f(12,12+4)= f(12,12)=4f(12,12)
f(12,12)=4f(12,12)
∵f(x,x)=x,∴f(12,12)=12
因此,f(12,16)=4f(12,12)=4×12=48
∵f(x,y)=f(y,x)
∴f(16,12)=f(12,16)=48,可得f(12,16)+f(16,12)=48+48=96
故选:A
点评:本题给出抽象函数,求特殊的函数值,着重考查了函数的定义、抽象函数及其应用等知识,属于基础题.
 f(x,y),从而得到f(12,16)=4f(12,12)=4×12=48,再结合f(x,y)=f(y,x)得f(16,12)=f(12,16)=48,从而得到f(12,16)+f(16,12)的值.
f(x,y),从而得到f(12,16)=4f(12,12)=4×12=48,再结合f(x,y)=f(y,x)得f(16,12)=f(12,16)=48,从而得到f(12,16)+f(16,12)的值.解答:解:∵(x+y)f(x,y)=yf(x,x+y),
∴f(x,x+y)=
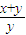 f(x,y),
f(x,y),因此,f(12,16)=f(12,12+4)=
 f(12,12)=4f(12,12)
f(12,12)=4f(12,12)∵f(x,x)=x,∴f(12,12)=12
因此,f(12,16)=4f(12,12)=4×12=48
∵f(x,y)=f(y,x)
∴f(16,12)=f(12,16)=48,可得f(12,16)+f(16,12)=48+48=96
故选:A
点评:本题给出抽象函数,求特殊的函数值,着重考查了函数的定义、抽象函数及其应用等知识,属于基础题.

练习册系列答案
相关题目
 }是否为等差数列,并说明理由.
}是否为等差数列,并说明理由.