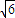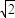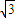题目内容
双曲线C的左右焦点分别为F1,F2,且F2恰为抛物线y2=4x的焦点,设双曲线C与该抛物线的一个交点为A,若△AF1F2是以AF1为底边的等腰三角形,则双曲线C的离心率为( )
|
| A. |
| B. | 1 | C. | 1 | D. | 2 |
考点:
双曲线的简单性质.
专题:
计算题;圆锥曲线的定义、性质与方程.
分析:
求出抛物线的焦点坐标,即可得到双曲线c的值,利用抛物线与双曲线的交点以及△AF1F2是以AF1为底边的等腰三角形,
结合双曲线a、b、c关系求出a的值,然后求出离心率.
解答:
解:抛物线的焦点坐标(1,0),所以双曲线中,c=1,
因为双曲线C与该抛物线的一个交点为A,若△AF1F2是以AF1为底边的等腰三角形,
由抛物线的定义可知,抛物线的准线方程过双曲线的左焦点,所以![]() ,
,
c2=a2+b2=1,解得a=![]() ,双曲线的离心率e=
,双曲线的离心率e=![]() =
=![]() =1+
=1+![]() .
.
故选B.
点评:
本题考查抛物线的简单性质以及双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
 的左右焦点分别是
的左右焦点分别是 ,设
,设 是双曲线右支上一点,
是双曲线右支上一点, 在
在 上投影的大小恰好为
上投影的大小恰好为 ,且它们的夹角为
,且它们的夹角为 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) B.
B. C.
C. D.
D.
 ,
, 分别是双曲线
分别是双曲线 =1的左右焦点,若以坐标原点O为圆心,
=1的左右焦点,若以坐标原点O为圆心, 为半径
为半径 ,则当△
,则当△ 的面积等于
的面积等于 时,双曲线的离心
时,双曲线的离心 B.
B.
 C.
C.
 D.
D.

 -
- =1(a>0,b>0)的左右焦点分别是F1、F2,过点F2的直线交双曲线右支于不同的两点M、N,若△MNF1为正三角形,则该双曲线的离心率为( )
=1(a>0,b>0)的左右焦点分别是F1、F2,过点F2的直线交双曲线右支于不同的两点M、N,若△MNF1为正三角形,则该双曲线的离心率为( )



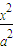 -
-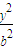 =1(a>0,b>0)的左右焦点分别是F1、F2,过点F2的直线交双曲线右支于不同的两点M、N,若△MNF1为正三角形,则该双曲线的离心率为( )
=1(a>0,b>0)的左右焦点分别是F1、F2,过点F2的直线交双曲线右支于不同的两点M、N,若△MNF1为正三角形,则该双曲线的离心率为( )