题目内容
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 是等边三角形.
是等边三角形.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,若
,若![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)
【解析】试题分析:(Ⅰ)由椭圆![]() 短轴上的顶点得
短轴上的顶点得![]() ,由
,由![]() 是正三角形得
是正三角形得![]() 即
即![]() ,从而求得方程;
,从而求得方程;
(Ⅱ)设![]() ,
, ![]() ,因为
,因为![]() ,所以
,所以![]() ,且
,且![]() ,从而得即
,从而得即![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,将
,将![]() 代入直线
代入直线![]() 的方程得到
的方程得到![]() ,即可得解.
,即可得解.
试题解析:
解:(Ⅰ)由题意![]() 是椭圆
是椭圆![]() 短轴上的顶点,所以
短轴上的顶点,所以![]() ,
,
因为![]() 是正三角形,
是正三角形,
所以![]() ,即
,即![]() .
.
由![]() ,所以
,所以![]() .
.
所以椭圆![]() 的标准方程是
的标准方程是![]() .
.

(Ⅱ)设![]() ,
, ![]() ,依题意有
,依题意有![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以![]() ,
, ![]() ,即
,即![]() .
.
因为点![]() 在椭圆上,所以
在椭圆上,所以![]() ,即
,即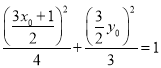 .
.
所以![]() ,解得
,解得![]() ,或
,或![]() .
.
因为线段![]() 与线段
与线段![]() 交于点
交于点![]() ,
,
所以![]() ,所以
,所以![]() .
.
因为直线![]() 的方程为
的方程为![]() ,
,
将![]() 代入直线
代入直线![]() 的方程得到
的方程得到![]() .
.
所以点![]() 的坐标为
的坐标为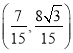 .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目