题目内容
设函数f(x)=|2x-1|,g(x)=|x-4|.(Ⅰ)解不等式f(x)<3;
(Ⅱ)解不等式f(x)+g(x)>4.
【答案】分析:(Ⅰ)|2x-1|<3?-3<2x-1<3,解出即可.
(Ⅱ)解不等式:|2x-1|+|x-4|>4,要分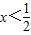 、
、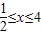 、x>4三种情况去讨论,分别解出即可.
、x>4三种情况去讨论,分别解出即可.
解答:解:(Ⅰ)∵|2x-1|<3,∴-3<2x-1<3,∴-1<x<2.
∴不等式f(x)<3的解集为{x|-1<x<2}.
(Ⅱ)∵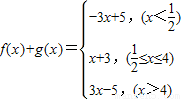 ,
,
①由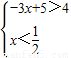 解得
解得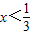 ;
;
②由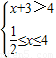 解得1<x≤4;
解得1<x≤4;
③由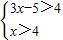 解得x>4.
解得x>4.
综上可知不等式f(x)+g(x)>4的解集为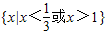 .
.
点评:分类讨论是解绝对值不等式最常用的方法,必须熟练掌握.
(Ⅱ)解不等式:|2x-1|+|x-4|>4,要分
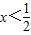 、
、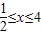 、x>4三种情况去讨论,分别解出即可.
、x>4三种情况去讨论,分别解出即可.解答:解:(Ⅰ)∵|2x-1|<3,∴-3<2x-1<3,∴-1<x<2.
∴不等式f(x)<3的解集为{x|-1<x<2}.
(Ⅱ)∵
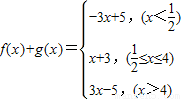 ,
,①由
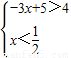 解得
解得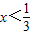 ;
;②由
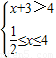 解得1<x≤4;
解得1<x≤4; ③由
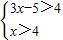 解得x>4.
解得x>4.综上可知不等式f(x)+g(x)>4的解集为
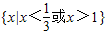 .
.点评:分类讨论是解绝对值不等式最常用的方法,必须熟练掌握.

练习册系列答案
相关题目