题目内容
已知点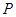 为椭圆
为椭圆 上异于左、右顶点的任意一点,
上异于左、右顶点的任意一点, 是左、右焦点,连接
是左、右焦点,连接 , 作D
, 作D 的旁切圆(与线段
的旁切圆(与线段 延长线及
延长线及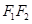 延长线均相切),其圆心为
延长线均相切),其圆心为 , 则动圆圆心
, 则动圆圆心 的轨迹所在曲线是( )
的轨迹所在曲线是( )
A.直线 B.圆 C.椭圆 D.双曲线
【答案】
A
【解析】解:如图画出圆M,切点分别为E、D、G,

由切线长相等定理知
F1G=F1E,PD=PE,F2D=F2G,
根据椭圆的定义知PF1+PF2=2a,
∴PF1+PF2=F1E+DF2(PD=PE)
=F1G+F2D(F1G=F1E)
=F1G+F2G=2a,
∴2F2G=2a-2c,F2G=a-c,
即点G与点A重合,
∴点M在x轴上的射影是长轴端点A,
M点的轨迹是垂直于x轴的一条直线(除去A点);
故选A.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 :
: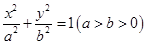 的离心率是
的离心率是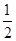 ,其左、右顶点分别为
,其左、右顶点分别为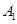 ,
,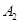 ,
,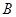 为短轴的端点,△
为短轴的端点,△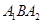 的面积为
的面积为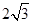 .
.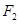 为椭圆
为椭圆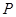 是椭圆
是椭圆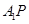 ,
,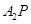 与直线
与直线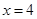 分别交于
分别交于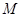 ,
,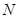 两点,证明:以
两点,证明:以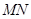 为直径的圆与直线
为直径的圆与直线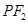 相切于点
相切于点