题目内容
设 是平面直角坐标系内x轴、y轴正方向上的单位向量,且
是平面直角坐标系内x轴、y轴正方向上的单位向量,且 ,则△ABC面积的值等于 .
,则△ABC面积的值等于 .
【答案】分析:由题意, 是平面直角坐标系内x轴、y轴正方向上的单位向量,且
是平面直角坐标系内x轴、y轴正方向上的单位向量,且 ,可得
,可得 由三角形面积公式知,可先由公式cos∠BAC=
由三角形面积公式知,可先由公式cos∠BAC= 求出两向量夹角余弦,再求出sin∠BAC,代入面积公式S△ABC=
求出两向量夹角余弦,再求出sin∠BAC,代入面积公式S△ABC=
 sin∠BAC,即可求出三角形的面积
sin∠BAC,即可求出三角形的面积
解答:解:由题意知
又cos∠BAC= =
= =
= ,
,
∴sin∠BAC=
又S△ABC=
 sin∠BAC=
sin∠BAC= ×2
×2 ×5×
×5× =5
=5
故答案为5
点评:本题考查向量在几何中的应用,考查了向量坐标的定义,向量夹角的坐标表示,向量模的坐标表示,同角三角函数关系,三角形面积公式,解题的关键是熟练掌握三角形的面积公式S△ABC=
 sin∠BAC,由公式确定出解题的方向先求出两向量的夹角.由题设条件得出两向量的坐标是本题的难点,理解向量坐标表示的定义是突破难点的关键.
sin∠BAC,由公式确定出解题的方向先求出两向量的夹角.由题设条件得出两向量的坐标是本题的难点,理解向量坐标表示的定义是突破难点的关键.
 是平面直角坐标系内x轴、y轴正方向上的单位向量,且
是平面直角坐标系内x轴、y轴正方向上的单位向量,且 ,可得
,可得 由三角形面积公式知,可先由公式cos∠BAC=
由三角形面积公式知,可先由公式cos∠BAC= 求出两向量夹角余弦,再求出sin∠BAC,代入面积公式S△ABC=
求出两向量夹角余弦,再求出sin∠BAC,代入面积公式S△ABC=
 sin∠BAC,即可求出三角形的面积
sin∠BAC,即可求出三角形的面积解答:解:由题意知

又cos∠BAC=
 =
= =
= ,
,∴sin∠BAC=

又S△ABC=

 sin∠BAC=
sin∠BAC= ×2
×2 ×5×
×5× =5
=5故答案为5
点评:本题考查向量在几何中的应用,考查了向量坐标的定义,向量夹角的坐标表示,向量模的坐标表示,同角三角函数关系,三角形面积公式,解题的关键是熟练掌握三角形的面积公式S△ABC=

 sin∠BAC,由公式确定出解题的方向先求出两向量的夹角.由题设条件得出两向量的坐标是本题的难点,理解向量坐标表示的定义是突破难点的关键.
sin∠BAC,由公式确定出解题的方向先求出两向量的夹角.由题设条件得出两向量的坐标是本题的难点,理解向量坐标表示的定义是突破难点的关键. 
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
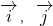 是平面直角坐标系内x轴、y轴正方向上的单位向量,且
是平面直角坐标系内x轴、y轴正方向上的单位向量,且 ,则△ABC面积的值等于________.
,则△ABC面积的值等于________.