Question

已知，点P（x，y）的坐标满足

3 x-y＜0 x- 3 y+2＜0 y≥0

，则

3 x+y

x2+y2

的取值范围为

[-

3

，

3

）

．

Answer 1

分析：作出题中不等式组表示的平面区域，P（x，y）为内部一点，设A（

3

2

，

1

2

），可得向量

OA

、

OP

的夹角θ∈（

π

6

，

5π

6

]，由向量的夹角公式可得

3 x+y

x2+y2

=2cosθ，由此结合余弦函数的单调性即可得到本题的答案．

解答：解：作出不等式组

3 x-y＜0 x- 3 y+2＜0 y≥0

表示的平面区域，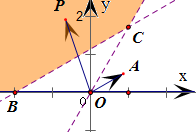
得到如图的平面区域，其中B（-2，0），C（1，

3

）
设A（

3

2

，

1

2

），P（x，y）为区域内一个动点，向量

OA

、

OP

的夹角为θ
∵|

OP

|=

x2+y2

，

OA

•

OP

=

3

2

x+

1

2

y
∴cosθ=

OA • OP

| OA |•| OP |

=

3 2 x+ 1 2 y

( 3 2 )2+( 1 2 )2 • x2+y2

=

1

2

×

3 x+y

x2+y2

∵当P运动到C点时，θ达到最小值；P运动到与x轴负半轴上一点重合时，θ达到最大值
∴∠AOC＜θ≤∠AOB，由直线OA、OC的倾斜角分别为

π

6

、

π

3

，可得θ∈（

π

6

，

5π

6

]
由此可得：-

3

2

≤cosθ＜

3

2

，即-

3

2

≤

1

2

×

3 x+y

x2+y2

＜

3

2

∴-

3

≤

3 x+y

x2+y2

＜

3

，即

3 x+y

x2+y2

的取值范围为[-

3

，

3

）
故答案为：[-

3

，

3

）

点评：本题给出二元一次不等式组表示的平面区域，求式子

3 x+y

x2+y2

的取值范围，着重考查了余弦函数的单调性、向量的夹角公式和简单线性规划的应用等知识，属于中档题．