题目内容

设（1+x）³+（1+x）⁴+（1+x）⁵+…+（1+x）⁵⁰=a₀+a₁x+…+a₅₀x⁵⁰，则a₃的值是（　　）

A、C₅₀⁴

B、2C₅₀³

C、C₅₁³

D、C₅₁⁴

分析：由题意可得a₃的值是x³的系数，而x³的系数为 C₃³+C₄³+C₅³+…+C₅₀³=C₄⁴+C₄³+C₅³+…+C₅₀³利用二项式系数的性质求得结果．

解答：解：由题意可得a₃的值是x³的系数，
而x³的系数为 C₃³+C₄³+C₅³+…+C₅₀³=C₄⁴+C₄³+C₅³+…+C₅₀³=C₅₁⁴，
故选D．

点评：本题考查二项式系数的性质的应用，求展开式中某项的系数，求出x³的系数为 C₃³+C₄³+C₅³+…+C₅₀³，是解题的关键．

练习册系列答案

小学课堂练习合肥工业大学出版社系列答案

设（1+x）³+（1+x）⁴+（1+x）⁵+…+（1+x）⁵⁰=a₀+a₁x+…+a₅₀x⁵⁰，则a₃的值是

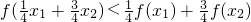设f（x）是定义在集合D上的函数，若对集合D中的任意两数x₁，x₂恒有 $数学公式$ 成立，则f（x）是定义在D上的β函数．
（1）试判断f（x）=x²是否是其定义域上的β函数？
（2）设f（x）是定义在R上的奇函数，求证：f（x）不是定义在R上的β函数．
（3）设f（x）是定义在集合D上的函数，若对任意实数α∈[0，1]以及集合D中的任意两数x₁，x₂恒有f（αx₁+（1-α）x₂）≤αf（x₁）+（1-α）f（x₂），则称f（x）是定义在D上的α-β函数．已知f（x）是定义在R上的α-β函数，m是给定的正整数，设a_n=f（n），n=1，2，3…m且a₀=0，a_m=2m，记∫=a₁+a₂+a₃+…+a_m，对任意满足条件的函数f（x），求∫的最大值．