题目内容

设a是正整数，a＜100，而且a3+23能被24整除，那么这样的a个数为（　　）
分析：由已知中a3+23即（a3-1）+24能被24整除，则（a3-1）也应该是24的倍数，利用立方差公式，我们可得a3-1=（a-1）（a2+a+1），根据a是正整数时，a2+a+1为奇数，不可能24的倍数，可得a-1为24的整数倍，进而得到答案．
解答：解：∵a3+23=（a3-1）+24
当a3+23能被24整除时，
a3-1=（a-1）（a2+a+1）也是24的倍数
∵当a是正整数时，a2+a+1为奇数，不可能24的倍数
故a-1为24的倍数时，即a的值为1，25，49，73，97时满足条件
故选B
点评：本题考查的知识点是整除的定义，其中根据已知条件确定出（a3-1）是24的倍数，并根据整除的性质，判断出a-1为24的倍数，是解答本题的关键．
练习册系列答案
相关题目
已知每项均是正整数的数列A：a1，a2，a3，…，an，其中等于i的项有ki个（i=1，2，3…），设bj=k1+k2+…+kj（j=1，2，3…），g（m）=b1+b2+…+bm-nm（m=1，2，3…）．
（Ⅰ）设数列A：1，2，1，4，求g（1），g（2），g（3），g（4），g（5）；
（Ⅱ）若数列A满足a1+a2+…+an-n=100，求函数g（m）的最小值．

设a是正整数，aº1(mod4)．

    求证： (nÎN)能被2n-1整除
设a是正整数，aº1(mod4)．

    求证： (nÎN)能被2n-1整除
已知每项均是正整数的数列A：a1，a2，a3，…，an，其中等于i的项有ki个（i=1，2，3…），设bj=k1+k2+…+kj（j=1，2，3…），g（m）=b1+b2+…+bm-nm（m=1，2，3…）．
（Ⅰ）设数列A：1，2，1，4，求g（1），g（2），g（3），g（4），g（5）；
（Ⅱ）若数列A满足a1+a2+…+an-n=100，求函数g（m）的最小值．
设A是满足下列两个条件的无穷数列{an}的集合：
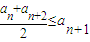①；     ②an≤M．其中n∈N*，M是与n无关的常数．
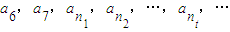（Ⅰ）若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，证明：{Sn}∈A；
（Ⅱ）对于（Ⅰ）中数列{an}，正整数n1，n2，…，nt…（t∈N*）满足7＜n1＜n2＜…＜nt＜…（t∈N*），并且使得成等比数列． 若bm=10m-nm（m∈N*），则{bm}∈A是否成立？若成立，求M的取值范围，若不成立，请说明理由；
（Ⅲ）设数列{cn}的各项均为正整数，且{cn}∈A，证明：cn≤cn+1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网