题目内容
已知数列{an}、{bn}都是公差为1的等差数列,其首项分别为a1、b1,且a1+b1=5,a1>b1,a1,b1∈N*(n∈N*),则数列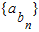 前10项的和等于( )
前10项的和等于( )A.55
B.70
C.85
D.100
【答案】分析:根据a1+b1=5,a1,b1∈N*,故可知a1,b1有3和2,4和1两种可能,又知数列{an},{bn}都是公差为1的等差数列,即可求出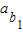 ,再根据等差数列的求和公式即可求出数列{
,再根据等差数列的求和公式即可求出数列{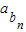 }的前10项和.
}的前10项和.
解答:解:∵a1+b1=5,a1,b1∈N*,a1>b1,a1,b1∈N*(n∈N*),
∴a1,b1有3和2,4和1两种可能,
当a1,b1为4和1的时,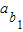 =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85;
当a1,b1为3和2的时,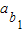 =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85;
故数列{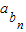 }的前10项和等于85,
}的前10项和等于85,
故选C.
点评:本题主要考查数列求和和等差数列的性质的知识点,解答本题的关键是对a1+b1=5进行两种可能分类,是基础题.
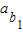 ,再根据等差数列的求和公式即可求出数列{
,再根据等差数列的求和公式即可求出数列{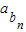 }的前10项和.
}的前10项和.解答:解:∵a1+b1=5,a1,b1∈N*,a1>b1,a1,b1∈N*(n∈N*),
∴a1,b1有3和2,4和1两种可能,
当a1,b1为4和1的时,
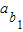 =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85; 当a1,b1为3和2的时,
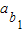 =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85;故数列{
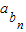 }的前10项和等于85,
}的前10项和等于85,故选C.
点评:本题主要考查数列求和和等差数列的性质的知识点,解答本题的关键是对a1+b1=5进行两种可能分类,是基础题.

练习册系列答案
相关题目