题目内容
【题目】若平面直角坐标系内两点![]() ,
,![]() 满足条件:①点
满足条件:①点![]() ,
,![]() 都在函数
都在函数![]() 的图像上;②点
的图像上;②点![]() ,
,![]() 关于原点对称.则称
关于原点对称.则称![]() 是函数
是函数![]() 的一个“伙伴点组”(点组
的一个“伙伴点组”(点组![]() 与
与![]() 看作同一个“伙伴点组”).已知函数
看作同一个“伙伴点组”).已知函数![]() 有两个“伙伴点组”,则实数
有两个“伙伴点组”,则实数![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]()
【解析】
由题意可知,“伙伴点组”的点满足:都在函数图像上,且关于坐标原点对称.将问题转化为函数![]() 的图像与直线
的图像与直线![]() 的交点个数为
的交点个数为![]() 即可.
即可.
由题意可知,“伙伴点组”的点满足:都在函数图像上,且关于坐标原点对称.
可作出函数![]() 关于原点对称的函数
关于原点对称的函数![]() 的图像(如图),使它与直线
的图像(如图),使它与直线![]() 的交点个数为
的交点个数为![]() 即可.
即可.

当直线![]() 与
与![]() 的图像相切时,设切点为
的图像相切时,设切点为![]() ,
,
又![]() 的导数为
的导数为![]() ,即
,即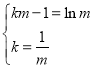
解得![]() 可得函数
可得函数![]() 的图像过点
的图像过点![]() 的切线的斜率为
的切线的斜率为![]() .
.
结合图像可知当![]() 时两个函数图像有两个交点.
时两个函数图像有两个交点.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目