Question

已知p:2x²-9x+a＜0,q:且p是q的充分条件,求实数a的取值范围.

Answer 1

解:利用等价转换思想把p和q的充分条件(pq)等价转换为p是q的必要条件(qp),然后利用集合与命题的关系和数轴进行观察,即可求得a的取值范围.

由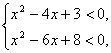得即2＜x＜3.

∴q:2＜x＜3.

设A={x|2x²-9x+a＜0},B={x|2＜x＜3},

∵pq,∴qp.

∴BA.

∴2＜x＜3包含于集合A,

即2＜x＜3满足不等式2x²-9x+a＜0.

∴2＜x＜3满足不等式a＜9x-2x².

∵当2＜x＜3时,9x-2x²=-2(x²x+)

=-2(x)²+∈(9,］,

即9＜9x-2x²≤,

∴a≤9.