题目内容
(本题满分14分) 设公比为正数的等比数列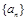 的前
的前 项和为
项和为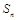 ,已知
,已知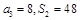 ,数列
,数列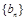 满足
满足 .
.
(Ⅰ)求数列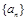 和
和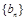 的通项公式;
的通项公式;
(Ⅱ)是否存在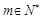 ,使得
,使得 是数列
是数列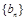 中的项?若存在,求出
中的项?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(Ⅰ)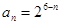 ,
,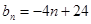
(Ⅱ)当t=-1或t=-2时,即m=5或m=6时, 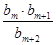 是数列
是数列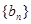 中的项
中的项
【解析】解:(Ⅰ)设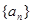 的公比为q,则有
的公比为q,则有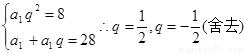
则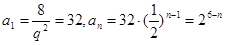 ,
,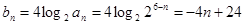 .
.
即数列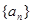 和
和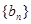 的通项公式为
的通项公式为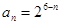 ,
,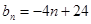 . ……6′
. ……6′
(Ⅱ)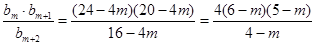 ,令
,令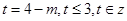 ,所以
,所以
 ,
,
如果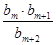 是数列
是数列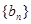 中的项,设为第
中的项,设为第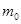 项,则有
项,则有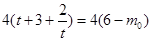 ,那么
,那么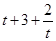 为小于等于5的整数,所以
为小于等于5的整数,所以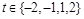 .
……4′
.
……4′
当t=1或t=2时, 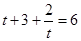 ,不合题意;
,不合题意;
当t=1或t=2时, 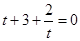 ,符合题意.
,符合题意.
所以,当t=-1或t=-2时,即m=5或m=6时, 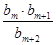 是数列
是数列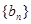 中的项. ……8
中的项. ……8
思路分析:第一问利用已知的项的关系式联立方程组可知公比,和首项,求解得到通项公式。
第二问中,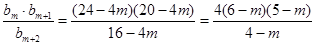 ,令
,令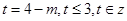 ,所以
,所以
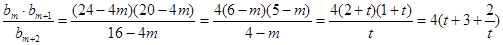 ,
,
如果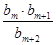 是数列
是数列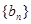 中的项,设为第
中的项,设为第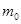 项,则有
项,则有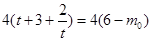 ,那么
,那么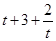 为小于等于5的整数,所以t=-2,-1,1,2
为小于等于5的整数,所以t=-2,-1,1,2
所以,当t=-1或t=-2时,即m=5或m=6时, 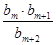 是数列
是数列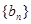 中的项.
中的项.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).