题目内容
设O为坐标原点,F1,F2是双曲线 -
- =1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1PF2=60°,|OP|=
=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1PF2=60°,|OP|= a,则该双曲线的离心率为
a,则该双曲线的离心率为
- A.

- B.

- C.2
- D.

A
分析:利用双曲线的定义与余弦定理可得到a2与c2的关系,从而可求得该双曲线的离心率.
解答:设该双曲线的离心率为e,依题意,||PF1|-|PF2||=2a,
∴ +
+ -2|PF1|•|PF2|=4a2,
-2|PF1|•|PF2|=4a2,
不妨设 +
+ =x,|PF1|•|PF2|=y,
=x,|PF1|•|PF2|=y,
上式为:x-2y=4a2,①
∵∠F1P F2=60°,
∴在△F1P F2中,由余弦定理得, =
= +
+ -2|PF1|•|PF2|•cos60°=4c2,②
-2|PF1|•|PF2|•cos60°=4c2,②
即x-y=4c2,②
又|OP|= a,
a, +
+ =2
=2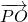 ,
,
∴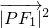 +
+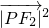 +2
+2 •
• ×cos60°=4
×cos60°=4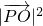 =7a2,
=7a2,
即 +
+ +|PF1|•|PF2|=7a2,
+|PF1|•|PF2|=7a2,
即x+y=7a2,③
由②+③得:2x=4c2+7a2,
①+③×2得:x=6a2,于是有4c2=5a2,
∴ =
= ,
,
∴e= =
= .
.
故选A.
点评:本题考查双曲线的定义与余弦定理的应用,得到a2与c2的关系是关键,也是难点,考查分析问题,解决问题的能力,属于中档题.
分析:利用双曲线的定义与余弦定理可得到a2与c2的关系,从而可求得该双曲线的离心率.
解答:设该双曲线的离心率为e,依题意,||PF1|-|PF2||=2a,
∴
 +
+ -2|PF1|•|PF2|=4a2,
-2|PF1|•|PF2|=4a2,不妨设
 +
+ =x,|PF1|•|PF2|=y,
=x,|PF1|•|PF2|=y,上式为:x-2y=4a2,①
∵∠F1P F2=60°,
∴在△F1P F2中,由余弦定理得,
 =
= +
+ -2|PF1|•|PF2|•cos60°=4c2,②
-2|PF1|•|PF2|•cos60°=4c2,②即x-y=4c2,②
又|OP|=
 a,
a, +
+ =2
=2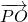 ,
,∴
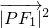 +
+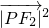 +2
+2 •
• ×cos60°=4
×cos60°=4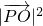 =7a2,
=7a2,即
 +
+ +|PF1|•|PF2|=7a2,
+|PF1|•|PF2|=7a2,即x+y=7a2,③
由②+③得:2x=4c2+7a2,
①+③×2得:x=6a2,于是有4c2=5a2,
∴
 =
= ,
,∴e=
 =
= .
.故选A.
点评:本题考查双曲线的定义与余弦定理的应用,得到a2与c2的关系是关键,也是难点,考查分析问题,解决问题的能力,属于中档题.

练习册系列答案
相关题目
设O为坐标原点,F1,F2是双曲线
-
=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1PF2=60°,|OP|=
a,则该双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
A、x±
| ||
B、
| ||
C、x±
| ||
D、
|