题目内容
设an=(2n+1)(3n+2),求它的前n项和Sn,并用数学归纳法证明结论.
解:S1=a1=15;?
S2=a1+a2=55;?
S3=a1+a2+a3=132.?
猜想Sn=![]() (4n3+13n2+13n).?
(4n3+13n2+13n).?
证明:(1)n=1时显然成立.?
(2)假设n=k时成立,即Sk=![]() (4k3+13k2+13k),?
(4k3+13k2+13k),?
则Sk+1=Sk+ak+1?
=![]() (4k3+13k2+13k)+(2k+3)(3k+5)?
(4k3+13k2+13k)+(2k+3)(3k+5)?
=![]() (4k3+13k2+13k)+6k2+19k+15?
(4k3+13k2+13k)+6k2+19k+15?
=![]() (4k3+25k2+51k+30)?
(4k3+25k2+51k+30)?
=![]() [4(k+1)3+13(k+1)2+13(k+1)].?
[4(k+1)3+13(k+1)2+13(k+1)].?
∴当n=k+1时也成立.?
由(1)(2)知,Sn=![]() (4n3+13n2+13n)对任意n∈N*成立.
(4n3+13n2+13n)对任意n∈N*成立.

练习册系列答案
相关题目
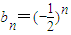 ,n∈N*,判断{an}、{bn}是否为“p-摆动数列”,并说明理由;
,n∈N*,判断{an}、{bn}是否为“p-摆动数列”,并说明理由; ,c1=1,求常数p的值;
,c1=1,求常数p的值;