题目内容
已知函数f(x)=x+alnx
(I)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)求f(x)的单调区间;
(III)若函数f(x)没有零点,求a的取值范围.
(I)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)求f(x)的单调区间;
(III)若函数f(x)没有零点,求a的取值范围.
分析:(Ⅰ)把a=1代入函数解析式,求出f(1)的值,求出f′(1)的值,然后直接代入直线方程的点斜式得切线方程;
(Ⅱ)求出原函数的导函数f′(x)=
(x>0),当a≥0时,在定义域内恒有f'(x)>0,∴f(x)的单调增区间是(0,+∞);当a<0时,由导函数的零点对定义域分段,判出在各区间段内导函数的符号,由导函数的符号判断原函数的单调性;
(Ⅲ)利用(Ⅱ)求出的函数的单调区间,分a≥0和a<0讨论,当a<0时求出原函数的最小值,由最小值大于0求解实数a的取值范围.
(Ⅱ)求出原函数的导函数f′(x)=
| x+a |
| x |
(Ⅲ)利用(Ⅱ)求出的函数的单调区间,分a≥0和a<0讨论,当a<0时求出原函数的最小值,由最小值大于0求解实数a的取值范围.
解答:解:(I)当a=1时,f(x)=x+lnx,f′(x)=1+
(x>0),
∴f(1)=1,f'(1)=2,
∴曲线y=f(x)在点(1,f(1))处的切线方程为2x-y-1=0;
(II)函数f(x)=x+alnx,f′(x)=
(x>0).
当a≥0时,在x∈(0,+∞)时f'(x)>0,∴f(x)的单调增区间是(0,+∞);
当a<0时,函数f(x)与f'(x)在定义域上的情况如下:
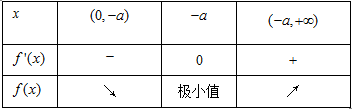
∴f(x)的单调减区间为(0,-a),单调增区间为(-a,+∞).
∴当a≥0时f(x)的单调增区间是(0,+∞);
当a<0时,f(x)的单调减区间为(0,-a),单调增区间为(-a,+∞).
(III)由(II)可知,
①当a>0时,(0,+∞)是函数f(x)的单调增区间,
且有f(e-
)=e-
-1<1-1=0,f(1)=1>0,
此时函数有零点,不符合题意;
②当a=0时,函数f(x)=x,在定义域(0,+∞)上没零点;
③当a<0时,f(-a)是函数f(x)的极小值,也是函数f(x)的最小值,
∴当f(-a)=a(ln(-a)-1)>0,即a>-e时,函数f(x)没有零点.
综上所述,当-e<a≤0时,f(x)没有零点.
| 1 |
| x |
∴f(1)=1,f'(1)=2,
∴曲线y=f(x)在点(1,f(1))处的切线方程为2x-y-1=0;
(II)函数f(x)=x+alnx,f′(x)=
| x+a |
| x |
当a≥0时,在x∈(0,+∞)时f'(x)>0,∴f(x)的单调增区间是(0,+∞);
当a<0时,函数f(x)与f'(x)在定义域上的情况如下:

∴f(x)的单调减区间为(0,-a),单调增区间为(-a,+∞).
∴当a≥0时f(x)的单调增区间是(0,+∞);
当a<0时,f(x)的单调减区间为(0,-a),单调增区间为(-a,+∞).
(III)由(II)可知,
①当a>0时,(0,+∞)是函数f(x)的单调增区间,
且有f(e-
| 1 |
| a |
| 1 |
| a |
此时函数有零点,不符合题意;
②当a=0时,函数f(x)=x,在定义域(0,+∞)上没零点;
③当a<0时,f(-a)是函数f(x)的极小值,也是函数f(x)的最小值,
∴当f(-a)=a(ln(-a)-1)>0,即a>-e时,函数f(x)没有零点.
综上所述,当-e<a≤0时,f(x)没有零点.
点评:本题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.考查了数学转化思想方法.该类问题在高考试卷中常以压轴题的形式出现.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|