Question

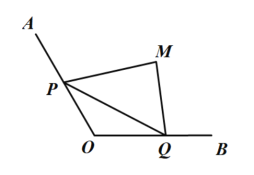
【题目】某沿海特区为了缓解建设用地不足的矛盾，决定进行围海造陆以增加陆地面积.如图，两海岸线，所成角为，现欲在海岸线，上分别取点，修建海堤，以便围成三角形陆地，已知海堤长为6千米.

（1）如何选择，的位置，使得的面积最大；

（2）若需要进一步扩大围海造陆工程，在海堤的另一侧选取点，修建海堤，围成四边形陆地.当海堤与的长度之和为10千米时，求四边形面积的最大值.

Answer 1

【答案】（1）当，两点距离点都为千米时，最大面积为（平方千米）；

（2）四边形面积的最大值为（平方千米）.

【解析】

（1）设，，由余弦定理得：，

因为，即，当且仅当时取得等号；

（2）要求四边形面积的最大值，只需求面积的最大值.在中，，所以点的轨迹是以，为焦点，长轴长10的椭圆（夹在两海岸线，区域内的曲线），根据椭圆的几何性质，求出点到距离的最大值即可得到最大面积.

（1）设，，（单位：千米）

在中，由余弦定理得：，

因为，，，，

所以，，

故，当且仅当时取得等号，

此时，（平方千米）.

所以，当，两点距离点都为千米时，的面积最大，最大面积为（平方千米）.

（2）由（1）知，要求四边形面积的最大值，只需求面积的最大值.

在中，，所以点的轨迹是以，为焦点，长轴长10的椭圆（夹在两海岸线，区域内的曲线），

以所在直线为轴，的垂直平分线为轴建立平面直角坐标系，

设点所在的椭圆方程为，焦距为，

由，得：，

所以点所在的椭圆方程为.

设，则，因为，

所以（平方千米），当且仅当（千米）时取得等号.

所以，四边形面积的最大值为（平方千米）.