题目内容
求圆(x-2)2+(y-4)2=1关于直线y=x+3对称的曲线的方程.
解析：由于圆关于直线对称的图象是一个与原来的圆等半径的圆,
可设所求圆的方程为［(x-2)2+(y-4)2-1］+λ(x-y+3)=0,?
即x2+y2+(λ-4)x+(-λ-8)y+(3λ+19)=0.?
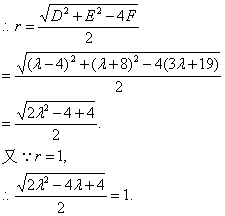
解之,得λ=0或λ=2.?
由于λ=0时即为已知圆C1,而C1的圆心O1(2,4)不在C2:y=x+3上,故所求的曲线C不可能是C1从而舍去,所以λ=2,代入原方程整理可得x2+y2-2x-10y+25=0,?
即(x-1)2+(y-5)2=1就是所要求的曲线的方程.
练习册系列答案
相关题目
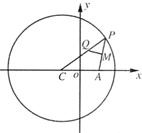已知C为圆