题目内容
设函数![]() 。(1)求
。(1)求![]() 的解析式;(2)证明:曲线
的解析式;(2)证明:曲线![]() 的图像是一个中心对称图形,并求其对称中心;(3)证明:曲线
的图像是一个中心对称图形,并求其对称中心;(3)证明:曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() 和直线
和直线![]() 所围三角形的面积为定值,并求出此定值。
所围三角形的面积为定值,并求出此定值。
解:
(Ⅰ)![]() ,
,
于是 解得
解得![]() 或
或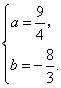
因![]() ,故
,故![]() .
.
(Ⅱ)证明:已知函数![]() ,
,![]() 都是奇函数.
都是奇函数.
所以函数![]() 也是奇函数,其图像是以原点为中心的中心对称图形.
也是奇函数,其图像是以原点为中心的中心对称图形.
而![]() .
.
可知,函数![]() 的图像按向量
的图像按向量![]() 平移,即得到函数
平移,即得到函数![]() 的图像,故函数
的图像,故函数![]() 的图像是以点
的图像是以点![]() 为中心的中心对称图形.
为中心的中心对称图形.
(Ⅲ)证明:在曲线上任取一点 .
.
由![]() 知,过此点的切线方程为
知,过此点的切线方程为
 .
.
令![]() 得
得![]() ,切线与直线
,切线与直线![]() 交点为
交点为 .
.
令![]() 得
得![]() ,切线与直线
,切线与直线![]() 交点为
交点为![]() .
.
直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
从而所围三角形的面积为 .
.
所以,所围三角形的面积为定值![]() .
.

练习册系列答案
相关题目
 ,曲线
,曲线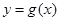 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点 处切线的斜率为
处切线的斜率为 C.
C. D.
D.
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点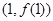 处切线的斜率为( )
处切线的斜率为( )  B.2 C.4
D.
B.2 C.4
D.
 ,曲线
,曲线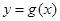 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点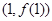 处切线的斜率为( )
处切线的斜率为( )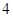 B.
B. C.
C. D.
D.
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线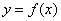 在点
在点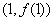 处的切线方程为 (
)
处的切线方程为 (
) B.
B. C.
C. D.
D.