题目内容
已知椭圆C: 的左、右焦点分别是F1、F2,离心率为e.直线l:y=ex+a与x轴、y轴分别交于A、B两点,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
的左、右焦点分别是F1、F2,离心率为e.直线l:y=ex+a与x轴、y轴分别交于A、B两点,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设 。
。
(1)证明: ;
;
(2)确定 的值,使得
的值,使得 是等腰三角形。
是等腰三角形。
(1)证法1:因为A、B分别是直线l:y=ex+a与x轴y轴的交点,所以A、B的坐标分别是
由 得
得 ,这里
,这里
所以点M的坐标是
由 得
得 ,
,
即 ,解得
,解得 .
.
证法2:因为A、B分别是直线l:y=ex+a与x轴y轴的交点,所以A、B的坐标分别是
设M的坐标为 ,由
,由 得
得 ,
,
所以 ,
,
因为点M在椭圆上,所以 ,
,
即 ,所以
,所以 ,
,
即 ,
,
解得 ,即
,即
(2)因为 ,
,
所以 为钝角,
为钝角,
要使 为等腰三角形,必有
为等腰三角形,必有 ,即
,即
设点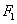 到l的距离为d,由
到l的距离为d,由
得
所以 ,于是
,于是
即当 ,
, 为等腰三角形.
为等腰三角形.
考点:直线与椭圆的位置关系,平面向量的坐标运算
点评:此题考查了直线与椭圆的位置关系,以及平面向量的坐标运算,关键是运算量较大

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,对任意的
,对任意的 ,给出以下四个结论:
,给出以下四个结论: ; ②
; ② ; ③
; ③ ; ④
; ④ ,其中正确的是( )
,其中正确的是( )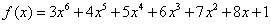 用秦九韶算法计算多
用秦九韶算法计算多  的一条斜线有一个平面与平面
的一条斜线有一个平面与平面 ”是“
”是“ ”的必要条件;
”的必要条件; ”的否定是“
”的否定是“ ”,“
”,“ ”,若
”,若 是
是 的充分不必要条件,则
的充分不必要条件,则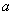 的取值范围是 .
的取值范围是 .
 .
. 在
在 上单调递减,求实数
上单调递减,求实数 ,求函数
,求函数 的极小值;
的极小值;  且
且 上有两个不同的极值点,求
上有两个不同的极值点,求 的最小值.
的最小值. ,如果
,如果 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )  B.
B. C.
C. D.
D.
 折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上。
折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上。

 平面
平面
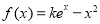 (其中
(其中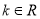 ,
,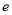 是自然对数的底数
是自然对数的底数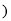
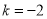 ,判断函数
,判断函数 在区间
在区间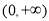 上的单调性;
上的单调性; 有两个极值点
有两个极值点 ,
,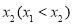 ,求
,求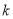 的取值范围;
的取值范围;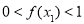 .
.