题目内容
定义在实数集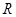 上的函数
上的函数 ,如果存在函数
,如果存在函数 (
( 为常数),使得
为常数),使得 对一切实数
对一切实数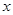 都成立,那么称
都成立,那么称 为函数
为函数 的一个承托函数.给出如下四个结论:
的一个承托函数.给出如下四个结论:
①对于给定的函数 ,其承托函数可能不存在,也可能有无数个;
,其承托函数可能不存在,也可能有无数个;
②定义域和值域都是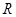 的函数
的函数 不存在承托函数;
不存在承托函数;
③ 为函数
为函数 的一个承托函数;
的一个承托函数;
④ 为函数
为函数 的一个承托函数.
的一个承托函数.
其中所有正确结论的序号是____________________.
①③
解析试题分析:由题意可知,如果存在函数 (
( 为常数),使得
为常数),使得 对一切实数
对一切实数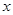 都成立,那么称
都成立,那么称 为函数
为函数 的一个承托函数,那么对于
的一个承托函数,那么对于 来说,不存在承托函数,当
来说,不存在承托函数,当 ,
, ,则此时有无数个承托函数;②定义域和值域都是
,则此时有无数个承托函数;②定义域和值域都是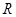 的函数
的函数 不存在承托函数,因为一个函数本身就是自己的承托函数.故错误;对于③因为
不存在承托函数,因为一个函数本身就是自己的承托函数.故错误;对于③因为
 恒成立,则可知
恒成立,则可知 为函数
为函数 的一个承托函数;成立;对于④如果
的一个承托函数;成立;对于④如果 为函数
为函数 的一个承托函数.则必然有
的一个承托函数.则必然有 并非对任意实数都成立,只有当
并非对任意实数都成立,只有当 或
或 时成立,因此错误;综上可知正确的序号为①③.
时成立,因此错误;综上可知正确的序号为①③.
考点:新定义.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 的所有零点之和为 .
的所有零点之和为 . 是首项为
是首项为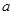 ,公差为1的等差数列,
,公差为1的等差数列, ,若对任意的
,若对任意的 ,都有
,都有 成立,则实数
成立,则实数
 的定义域是 .
的定义域是 .
 ,若关于
,若关于 的方程
的方程 有三个不同的实根,则实数
有三个不同的实根,则实数 的取值范围是.
的取值范围是. (K为给定常数),已知函数
(K为给定常数),已知函数 ,若对于任意的
,若对于任意的 ,恒有
,恒有 ,则实数K的取值范围为 .
,则实数K的取值范围为 . 是定义在
是定义在 上的奇函数,若它的最小正周期为
上的奇函数,若它的最小正周期为 ,则
,则 ________
________ 的定义域为__________。
的定义域为__________。 ,则函数
,则函数 的零点个数为 个.
的零点个数为 个.