题目内容
 (2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
(2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )分析:求出阴影部分的面积即可,连接OC,把下面的阴影部分平均分成了2部分,然后利用位移割补的方法,分别平移到图中划线部分,那么阴影部分的面积就是图中扇形的面积-直角三角形AOB的面积.
解答: 解:本题的测度是面积
解:本题的测度是面积
设扇形的半径为r,则扇形OAB的面积为
πr2
连接OC,把下面的阴影部分平均分成了2部分,然后利用位移割补的方法,分别平移到图中划线部分,则阴影部分的面积为:
πr2-
r2,
∴此点取自阴影部分的概率是
=1-
故选C.
 解:本题的测度是面积
解:本题的测度是面积设扇形的半径为r,则扇形OAB的面积为
| 1 |
| 4 |
连接OC,把下面的阴影部分平均分成了2部分,然后利用位移割补的方法,分别平移到图中划线部分,则阴影部分的面积为:
| 1 |
| 4 |
| 1 |
| 2 |
∴此点取自阴影部分的概率是
| ||||
|
| 2 |
| π |
故选C.
点评:本题考查几何概型,解题的关键是利用位移割补的方法求组合图形面积,此类不规则图形的面积可以转化为几个规则的图形的面积的和或差的计算.

练习册系列答案
相关题目
 (2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=
(2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ= (2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
(2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )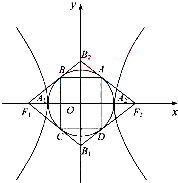 (2012•湖北)如图,双曲线
(2012•湖北)如图,双曲线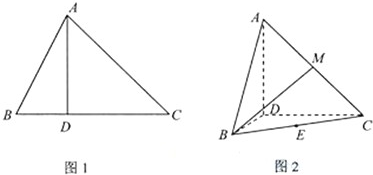 (2012•湖北)如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示),
(2012•湖北)如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示),