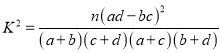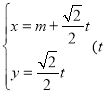题目内容
【题目】已知椭圆![]() 的中心在坐标原点,长轴在
的中心在坐标原点,长轴在![]() 轴上,
轴上,![]() 分别在其左、右焦点,
分别在其左、右焦点,![]() 在椭圆上任意一点,且
在椭圆上任意一点,且![]() 的最大值为1,最小值为
的最大值为1,最小值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的右顶点,直线
的右顶点,直线![]() 是与椭圆交于
是与椭圆交于![]() 两点的任意一条直线,若
两点的任意一条直线,若![]() ,证明直线
,证明直线![]() 过定点.
过定点.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)借助题设条件运用向量的数量积公式建立方程组求解;(2)依据题设运用直线与椭圆的位置关系探求.
试题解析:
(1)设椭圆方程为![]() ,
,![]() 为椭圆上任意一点,
为椭圆上任意一点,
所以![]() ,
,![]() ,所以
,所以
![]() ,…………………………………………2分
,…………………………………………2分
又因为![]() ,所以
,所以
![]() .……………………4分
.……………………4分
因为![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() ,
,
因此![]() ,
,
所以椭圆方程为![]() …………………………6分
…………………………6分
(2)①若直线![]() 不垂直于
不垂直于![]() 轴,设该直线方程为
轴,设该直线方程为![]() ,
,![]() ,
,
由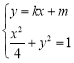 ,得
,得![]() ,
,
化简得![]() ,
,
所以![]() ,
,![]() ,…………………………7分
,…………………………7分
![]()
![]() .………8分
.………8分
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
去分母得![]()
即![]() .…………………………10分
.…………………………10分
![]() ,所以
,所以![]() 或
或![]() ,
,
当![]() 时,
时,![]() 过定点
过定点![]() ,显然不满足题意;
,显然不满足题意;
当![]() 时,
时,![]() 过定点
过定点![]() .
.
②若直线![]() 垂直于
垂直于![]() 轴,设
轴,设![]() 与
与![]() 轴交于点
轴交于点![]() ,由椭圆的对称性可知
,由椭圆的对称性可知![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() ,化简得
,化简得![]() ,
,
解得![]() 或2(舍),即此时直线
或2(舍),即此时直线![]() 也过定点
也过定点![]() .
.
综上直线![]() 过定点
过定点![]() .…………………………13分
.…………………………13分

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R(x)=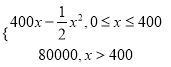 其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
男性用户:
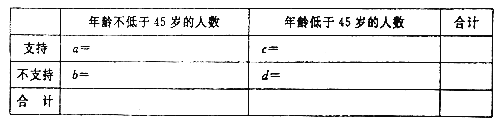
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.