题目内容
14.(1)已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,求实数a的取值范围.(2)若函数f(x)是定义在[-1,1]上的增函数,且f(a)<f(2-3a),求实数a的取值范围.
分析 (1)f(x)=x2+2(a-1)x+2的图象是开口朝上,且以直线x=1-a为对称轴的抛物线,若函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,则1-a≥4,解得答案;
(2)由函数f(x)是定义在[-1,1]上的增函数,若f(a)<f(2-3a),则-1≤a<2-3a≤1,解得答案;
解答 解:(1)f(x)=x2+2(a-1)x+2的图象是开口朝上,且以直线x=1-a为对称轴的抛物线,
若函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,
则1-a≥4.
解得:a∈(-∞,-3],
(2)∵函数f(x)是定义在[-1,1]上的增函数,
若f(a)<f(2-3a),
则-1≤a<2-3a≤1,
解得:a∈[$\frac{1}{3}$,$\frac{1}{2}$]
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目

 的值
的值 ,b=2,求△ABC的面积S.
,b=2,求△ABC的面积S.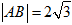 ,则圆C的内接正三角形的面积为( )
,则圆C的内接正三角形的面积为( )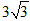 D.
D. 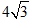
 若f[f(a)]≤2,则实数a的取值范围是
若f[f(a)]≤2,则实数a的取值范围是