题目内容
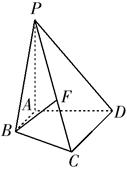
如图,已知四棱锥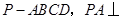 平面
平面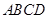 ,底面
,底面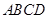 为直角梯形,
为直角梯形,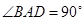 ,且
,且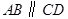 ,
,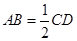 .
.
(1)点 在线段
在线段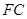 上运动,且设
上运动,且设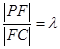 ,问当
,问当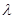 为何值时,
为何值时,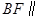 平面
平面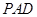 ,并证明你的结论;
,并证明你的结论;
(2)当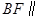 面
面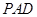 ,且
,且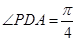 ,
,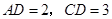 求四棱锥
求四棱锥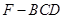 的体积.
的体积.
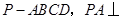 平面
平面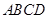 ,底面
,底面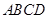 为直角梯形,
为直角梯形,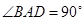 ,且
,且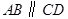 ,
,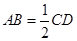 .
.
(1)点
 在线段
在线段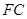 上运动,且设
上运动,且设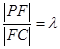 ,问当
,问当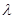 为何值时,
为何值时,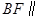 平面
平面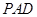 ,并证明你的结论;
,并证明你的结论;(2)当
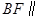 面
面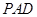 ,且
,且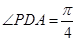 ,
,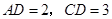 求四棱锥
求四棱锥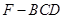 的体积.
的体积.(1)见解析;(2) .
.
 .
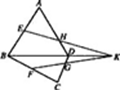
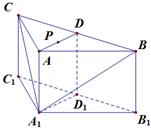
.试题分析:(1)取PD中点G,连接AG、FG,证明
 即可;(2)由条件可得
即可;(2)由条件可得 为等腰直角三角形,利用三棱锥的体积公式计算即可.
为等腰直角三角形,利用三棱锥的体积公式计算即可.试题解析::(1)当
 时,取PD中点G,连接AG、FG,则
时,取PD中点G,连接AG、FG,则
∴
 且
且 平面
平面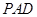 ∴
∴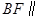 平面
平面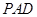
(2)∵
 平面
平面 且
且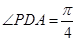 ∴
∴ 为等腰直角三角形
为等腰直角三角形∴


练习册系列答案
相关题目
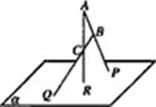
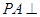 平面
平面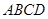 ,四边形
,四边形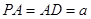 ,M,N分别是AB,PC的中点,
,M,N分别是AB,PC的中点,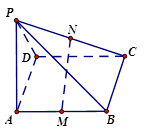
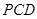 和平面
和平面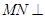 平面
平面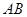 的长度变化时,求异面直线PC与AD所成角的可能范围.
的长度变化时,求异面直线PC与AD所成角的可能范围.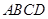 为矩形,平面
为矩形,平面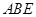 ,
,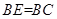 ,
,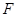 为
为 上的一点,且
上的一点,且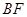 ⊥平面
⊥平面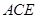 .
. 
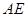 ⊥
⊥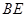 ;
; .
.
 的6个顶点都在球
的6个顶点都在球 的球面上,若
的球面上,若
 ,
, ,则球
,则球




 和一个正八面体
和一个正八面体 ,把它们拼起来,使面
,把它们拼起来,使面 重合,则所得多面体是( )
重合,则所得多面体是( )