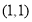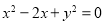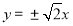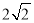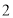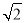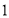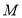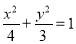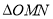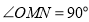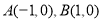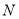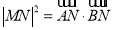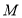题目内容
已知抛物线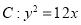 ,点
,点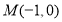 ,过
,过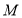 的直线
的直线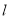 交抛物线
交抛物线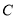 于
于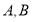 两点.
两点.
(1)若线段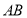 中点的横坐标等于
中点的横坐标等于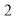 ,求直线
,求直线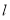 的斜率;
的斜率;
(2)设点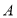 关于
关于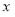 轴的对称点为
轴的对称点为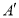 ,求证:直线
,求证:直线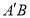 过定点.
过定点.
(1)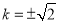 ;(2)
;(2)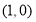
【解析】
试题分析:(1)因为点M在抛物线外面,所以过M与抛物线相交的直线斜率存在,用点斜式假设直线方程并联立抛物线方程,消去y,即可得一个关于x的一元二次方程,由韦达定理及已知中点的横坐标,即可求出斜率的值.
(2)由点A,B的横坐标满足(1)式中的一元二次方程,由韦达定理可得根与系数的等式,再写出直线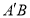 的方程,利用点差法将点A,B的坐标带入抛物线方程.即可求出直线过定点,要做点是否存在的判定.
的方程,利用点差法将点A,B的坐标带入抛物线方程.即可求出直线过定点,要做点是否存在的判定.
试题解析:(1)设过点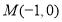 的直线方程为
的直线方程为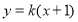 ,
,
由  得
得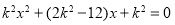
因为 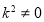 ,且
,且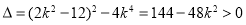 ,
,
所以,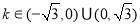 .
.
设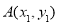 ,
,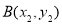 ,则
,则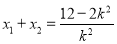 ,
,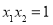 .
.
因为线段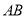 中点的横坐标等于
中点的横坐标等于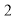 ,所以
,所以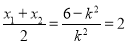 ,
,
解得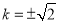 ,符合题意.
,符合题意.
(2)依题意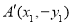 ,直线
,直线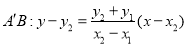 ,
,
又 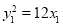 ,
,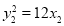 ,
,
所以 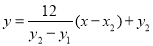
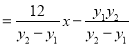
因为 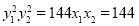 , 且
, 且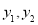 同号,所以
同号,所以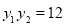 ,
,
所以 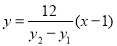 ,
,
所以,直线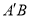 恒过定点
恒过定点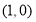 .
.
考点:1.直线与抛物线的位置关系.2.解方程的能力.3.恒过定点的问题.4.直线方程的表示.

练习册系列答案
相关题目