题目内容
设函数![]()
(Ⅰ)若![]() 在
在![]() 时有极值,求实数
时有极值,求实数![]() 的值和
的值和![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 在定义域上是增函数,求实数
在定义域上是增函数,求实数![]() 的取值范围.
的取值范围.
(Ⅰ)![]()
![]() 在
在![]() 时有极值,
时有极值,![]() 有
有![]() , …………………… 2分
, …………………… 2分
又![]() ,
,![]() 有
有![]() ,
,![]()
![]() ……………………5分
……………………5分
![]() 有
有![]()
![]() ,
,
由![]() 有
有![]() , ……………………7分
, ……………………7分
又![]()
![]()
![]() 关系有下表
关系有下表
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| 递增 | 递减 | 递增 |
![]()
![]() 的递增区间为
的递增区间为![]() 和
和 ![]() , 递减区间为
, 递减区间为![]() ……………………9分
……………………9分
(Ⅱ)若![]() 在定义域上是增函数,则
在定义域上是增函数,则![]() 在
在![]() 时恒成立,……………………10分
时恒成立,……………………10分
![]()
![]() ,
,![]() 需
需![]() 时
时![]() 恒成立,………11分
恒成立,………11分
化为![]() 恒成立,
恒成立,![]()
 ,
,![]() 需
需![]() ,此为所求。…………14分
,此为所求。…………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

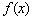
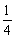

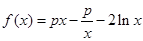 .
.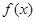 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数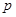 的取值范围;
的取值范围;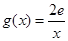 ,且
,且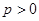 ,若在
,若在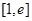 上至少存在一点
上至少存在一点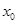 ,使得
,使得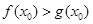 成立,求实数
成立,求实数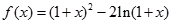 。
。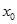 ,使不等式
,使不等式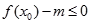 能成立,求实数
能成立,求实数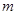 的最小值;
的最小值;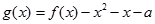 在区间
在区间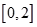 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数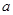 的取值范围。
的取值范围。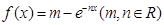
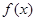 在点x=0处的切线方程为y=x,求m,n的值。
在点x=0处的切线方程为y=x,求m,n的值。 求a的取值范围.
求a的取值范围.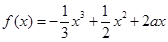 ,
,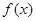 在
在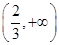 上存在单调增区间,求实数
上存在单调增区间,求实数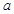 的取值范围;
的取值范围;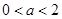 时
时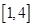 上的最小值为
上的最小值为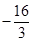 ,求
,求