题目内容
设函数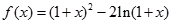 。
。
(Ⅰ)若在定义域内存在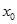 ,使不等式
,使不等式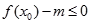 能成立,求实数
能成立,求实数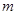 的最小值;
的最小值;
(Ⅱ)若函数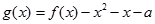 在区间
在区间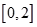 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数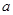 的取值范围。
的取值范围。
【答案】
(1)1;(2)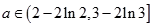
【解析】
试题分析:(1)不等式转化为: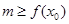 能成立,求m最小值。可以转化成求函数
能成立,求m最小值。可以转化成求函数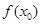 在定义域内的最小值。(2)函数
在定义域内的最小值。(2)函数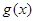 在
在 上有两个不同零点,所以
上有两个不同零点,所以 在
在 上有两个不同的解,可以令
上有两个不同的解,可以令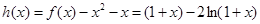 ,结合图形研究函数
,结合图形研究函数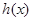 的性质即可。
的性质即可。
解答过程:(Ⅰ)要使得不等式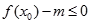 能成立,只需
能成立,只需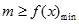 。 ………………1分
。 ………………1分
求导得: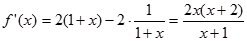 ,…………………………………2分
,…………………………………2分
∵函数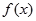 的定义域为
的定义域为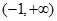 , ……………………………………3分
, ……………………………………3分
当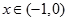 时,
时,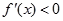 ,∴函数
,∴函数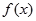 在区间
在区间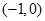 上是减函数;
上是减函数;
当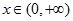 时,
时,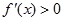 ,∴函数
,∴函数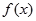 在区间(0,+∞)上是增函数。 …………5分
在区间(0,+∞)上是增函数。 …………5分
∴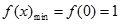 , ∴
, ∴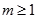 。故实数
。故实数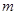 的最小值为1。……………………6分(Ⅱ)由
的最小值为1。……………………6分(Ⅱ)由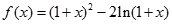 得:
得:
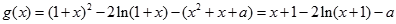 …………………7分
…………………7分
由题设可得:方程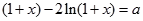 在区间
在区间 上恰有两个相异实根。
上恰有两个相异实根。
设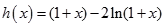 。∵
。∵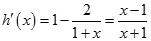 ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
|
减函数 |
|
增函数 |
|
∵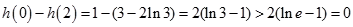 ,∴
,∴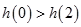 。
。
从而有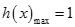 ,
,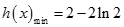
画出函数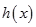 在区间
在区间 上的草图(见图),
上的草图(见图),

易知要使方程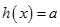 在区间
在区间 上恰有两个相异实根,
上恰有两个相异实根,
只需: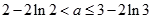 ,即:
,即: 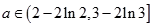 。 ……………12分
。 ……………12分
考点:本题考查了含参函数中参数的转化问题,将存在性问题转化为函数的最值和函数性质的研究,还需要借助图象工具,数形结合,为一道水平较高的题目。
点评:本题需要灵活转化,还要有一定逻辑分析能力和一定的计算能力,在难度上属于中等偏上,第一问计算简单,第二步计算在能力要求上有所增加。

练习册系列答案
相关题目








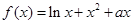 。
。 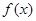 在
在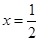 处取得极值,求
处取得极值,求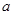 的值;
的值;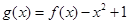 ,当
,当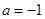 时,
时,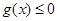 在其定义域内恒成立;
在其定义域内恒成立; 。
。