题目内容
【题目】已知抛物线
（
是正常数）上有两点
、
，焦点
，
甲：
；
乙：
；
丙：
；
丁：
.
以上是“直线
经过焦点”的充要条件有几个（ ）
A.
B.
C.
D.
【答案】B
【解析】
设直线
的方程为
，将直线的方程与抛物线的方程联立，利用韦达定理验证四个选项结论成立时，实数
的值，可以得出“直线经过焦点
”的充要条件的个数.
设直线的方程为，则直线交
轴于点
，且抛物线的焦点的坐标为
.
将直线的方程与抛物线的方程联立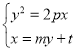
，消去得，
，
由韦达定理得
，
.
对于甲条件，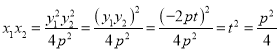
，得
，
甲条件是“直线经过焦点”的必要不充分条件；
对于乙条件，
，得
，此时，直线过抛物线的焦点，
乙条件是“直线经过焦点”的充要条件；
对于丙条件，
，即
，
解得或
，所以，丙条件是“直线经过焦点”的必要不充分条件；
对于丁条件，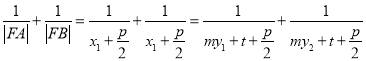
，
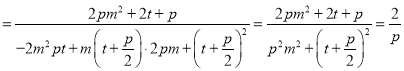化简得
，得，所以，丁条件是“直线经过焦点”的必要不充分条件.
综上所述，正确的结论只有
个，故选：B.
练习册系列答案
相关题目
