题目内容

在三棱柱ABC-A1B1C1中，底面为棱长为1的正三角形，侧棱AA1⊥底面ABC，点D在棱BB1上，且BD=1，若AD与平面AA1C1C所成的角为α，则sinα的值是（　　）
A、
3
2
B、
2
2
C、
10
4
D、
6
4
分析：建立空间直角坐标系，求出平面AA1C1C的一个法向量是
n
，和
AD
，计算cos＜
n
，
AD
＞即可求解sinα，
解答：精英家教网解：如图，建立坐标系，易求点D（
3
2
，
1
2
，1），
平面AA1C1C的一个法向量是
n
=（1，0，0），
所以cos＜
n
，
AD
＞=
3
2
2
=
6
4
，
即sinα=
6
4
．
故选D．
点评：本题考查用空间向量求直线与平面的夹角，考查计算能力，是基础题．
练习册系列答案
相关题目
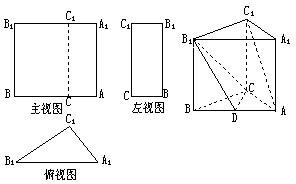精英家教网已知三棱柱ABC-A1B1C1的三视图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，cos∠A1=
35
．
（1）在三棱柱ABC-A1B1C1中，求证：BC⊥AC1；
（2）在三棱柱ABC-A1B1C1中，若D是底边AB的中点，求证：AC1∥平面CDB1．
（3）若三棱柱的高为5，求三视图中左视图的面积．
精英家教网如图：在正三棱柱ABC-A1 B1 C1中，AB=
AA13
=a，E，F分别是BB1，CC1上的点且BE=a，CF=2a．
（Ⅰ）求证：面AEF⊥面ACF；
（Ⅱ）求三棱锥A1-AEF的体积．
在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
5
，BC=4，在A1在底面ABC的投影是线段BC的中点O．
（1）求点C到平面A1ABB1的距离；
（2）求二面角A-BC1-B1的余弦值；
（3）若M，N分别为直线AA1，B1C上动点，求MN的最小值．
（2012•江西）在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
5
，BC=4，在A1在底面ABC的投影是线段BC的中点O．
（1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；
（2）求平面A1B1C与平面BB1C1C夹角的余弦值．
（2013•北京）如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1-BC1-B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求
BDBC1
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网