题目内容
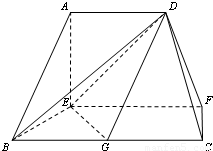
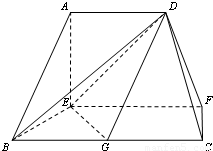
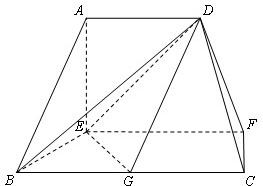
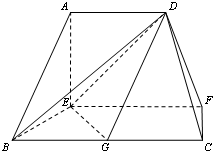
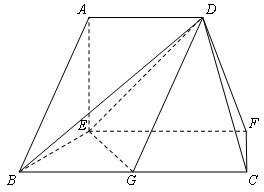 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.(Ⅰ) 求证:AB∥平面DEG;
(Ⅱ) 求证:BD⊥EG;
(Ⅲ) 求二面角C-DF-E的余弦值.
分析:(Ⅰ) 先证明四边形ADGB是平行四边形,可得AB∥DG,从而证明AB∥平面DEG.
(Ⅱ) 过D作DH∥AE交EF于H,则DH⊥平面BCFE,DH⊥EG,再证BH⊥EG,从而可证EG⊥平面BHD,故BD⊥EG.
(Ⅲ)分别以 EB、EF、EA为x轴、y轴、z轴,建立空间坐标系,由已知得
=(2,0,0)是平面EFDA的法向量.
求出平面DCF的法向量为n=(x,y,z),则由cosθ=cos<n,
>求得 二面角C-DF-E的余弦值.
(Ⅱ) 过D作DH∥AE交EF于H,则DH⊥平面BCFE,DH⊥EG,再证BH⊥EG,从而可证EG⊥平面BHD,故BD⊥EG.
(Ⅲ)分别以 EB、EF、EA为x轴、y轴、z轴,建立空间坐标系,由已知得
| EB |
求出平面DCF的法向量为n=(x,y,z),则由cosθ=cos<n,
| EB |
解答:解:(Ⅰ)证明:∵AD∥EF,EF∥BC,∴AD∥BC. 又∵BC=2AD,G是BC的中点,∴AD
BG,
∴四边形ADGB是平行四边形,∴AB∥DG.∵AB?平面DEG,DG?平面DEG,∴AB∥平面DEG.
(Ⅱ)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,
∴AE⊥平面BCFE. 过D作DH∥AE交EF于H,则DH⊥平面BCFE.∵EG?平面BCFE,∴DH⊥EG.
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG. 又BH∩DH=H,BH?平面BHD,DH?平面BHD,∴EG⊥平面BHD.
∵BD?平面BHD,∴BD⊥EG.
(Ⅲ)分别以 EB、EF、EA为x轴、y轴、z轴,建立空间坐标系,由已知得
=(2,0,0)
是平面EFDA的法向量.设平面DCF的法向量为n=(x,y,z),∵
=(0,-1,2),
=(2,1,0),
∴
,即
,令z=1,得n=(-1,2,1). 设二面角C-DF-E的大小为θ,
则cosθ=cos<n,
>=
=-
,∴二面角C-DF-E的余弦值为-
.
| ||
. |
∴四边形ADGB是平行四边形,∴AB∥DG.∵AB?平面DEG,DG?平面DEG,∴AB∥平面DEG.
(Ⅱ)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,
∴AE⊥平面BCFE. 过D作DH∥AE交EF于H,则DH⊥平面BCFE.∵EG?平面BCFE,∴DH⊥EG.
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG. 又BH∩DH=H,BH?平面BHD,DH?平面BHD,∴EG⊥平面BHD.
∵BD?平面BHD,∴BD⊥EG.
(Ⅲ)分别以 EB、EF、EA为x轴、y轴、z轴,建立空间坐标系,由已知得
| EB |
是平面EFDA的法向量.设平面DCF的法向量为n=(x,y,z),∵
| FD |
| FC |
∴
|
|
则cosθ=cos<n,
| EB |
| -2 | ||
2
|
| ||
| 6 |
| ||
| 6 |

点评:本题考查证明线面平行、线线垂直的方法,用向量法求二面角C-DF-E的余弦值,是解题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. (2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3
(2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3