题目内容
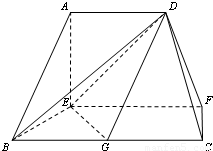
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.(Ⅰ) 求证:AB∥平面DEG;
(Ⅱ) 求二面角C-DF-E的余弦值.
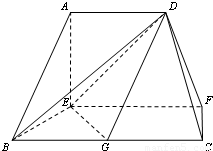
【答案】分析:(Ⅰ)由AD∥EF,EF∥BC,知AD∥BC.由BC=2AD,G是BC的中点,知四边形ADGB是平行四边形,由此能证明AB∥平面DEG.
(Ⅱ)由EF⊥平面AEB,AE?平面AEB,BE?平面AEB,知EF⊥AE,EF⊥BE,由AE⊥EB,知EB,EF,EA两两垂直.以点E为坐标原点,EB,EF,EA分别为x,y,z轴建立空间直角坐标系,利用向量法能够求出二面角C-DF-E的余弦值.
解答: (Ⅰ)证明:∵AD∥EF,EF∥BC,
(Ⅰ)证明:∵AD∥EF,EF∥BC,
∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴ ,
,
∴四边形ADGB是平行四边形,∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,
∴AB∥平面DEG.…(6分)
(Ⅱ)解:∵EF⊥平面AEB,AE?平面AEB,BE?平面AEB,
∴EF⊥AE,EF⊥BE,
又∵AE⊥EB,∴EB,EF,EA两两垂直.…(7分)
以点E为坐标原点,EB,EF,EA分别为x,y,z轴建立空间直角坐标系,
由已知得A(0,0,2),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2),G(2,2,0),
由已知得 =(2,0,0)是平面EFDA的法向量,
=(2,0,0)是平面EFDA的法向量,
设平面DCF的法向量 =(x,y,z),
=(x,y,z),
∵ =(0,-1,2),
=(0,-1,2), =(2,1,0),
=(2,1,0),
∴ ,解得
,解得 =(-1,2,1).
=(-1,2,1).
设二面角C-DF-E的平面角为θ,
则cosθ=cos< ,
, >=
>= =-
=- .
.
∴二面角C-DF-E的余弦值为- .
.
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,仔细解答,注意向量法的合理运用.
(Ⅱ)由EF⊥平面AEB,AE?平面AEB,BE?平面AEB,知EF⊥AE,EF⊥BE,由AE⊥EB,知EB,EF,EA两两垂直.以点E为坐标原点,EB,EF,EA分别为x,y,z轴建立空间直角坐标系,利用向量法能够求出二面角C-DF-E的余弦值.
解答:
 (Ⅰ)证明:∵AD∥EF,EF∥BC,
(Ⅰ)证明:∵AD∥EF,EF∥BC,∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴
 ,
,∴四边形ADGB是平行四边形,∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,
∴AB∥平面DEG.…(6分)
(Ⅱ)解:∵EF⊥平面AEB,AE?平面AEB,BE?平面AEB,
∴EF⊥AE,EF⊥BE,
又∵AE⊥EB,∴EB,EF,EA两两垂直.…(7分)
以点E为坐标原点,EB,EF,EA分别为x,y,z轴建立空间直角坐标系,
由已知得A(0,0,2),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2),G(2,2,0),
由已知得
 =(2,0,0)是平面EFDA的法向量,
=(2,0,0)是平面EFDA的法向量,设平面DCF的法向量
 =(x,y,z),
=(x,y,z),∵
 =(0,-1,2),
=(0,-1,2), =(2,1,0),
=(2,1,0),∴
 ,解得
,解得 =(-1,2,1).
=(-1,2,1).设二面角C-DF-E的平面角为θ,
则cosθ=cos<
 ,
, >=
>= =-
=- .
.∴二面角C-DF-E的余弦值为-
 .
.点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
相关题目
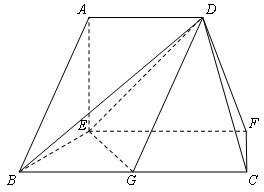 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.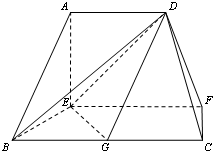 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. (2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3
(2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3