题目内容
【题目】已知椭圆C： 
+ 
=1（a＞b＞0）的离心率为 
，若圆x2+y2=a2被直线x﹣y﹣ 
=0截得的弦长为2
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知点A、B为动直线y=k（x﹣1），k≠0与椭圆C的两个交点，问：在x轴上是否存在定点M，使得 
为定值？若存在，试求出点M的坐标和定值；若不存在，请说明理由．
【答案】解：（I）圆x2+y2=a2的圆心（0，0）到直线x﹣y﹣ 
=0的距离d= 
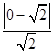=1，
∴2=2 
，解得a2=2，又 
= 
，a2=b2+c2，
联立解得：a2=2，c=1=b．
∴椭圆C的标准方程为： 
+y2=1．
（II）假设在x轴上存在定点M（m，0），使得 
为定值．
设A（x1，y1），B（x2，y2），联立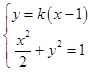 
，化为：（1+2k2）x2﹣4k2x+2k2﹣2=0，
则x1+x2= 
，x1x2= 
．
=（x1﹣m，y1）（x2﹣m，y2）=（x1﹣m）（x2﹣m）+y1y2=（x1﹣m）（x2﹣m）+k2（x1﹣1）（x2﹣1）=（1+k2）x1x2﹣（m+k2）（x1+x2）+m2+k2
=（1+k2） ﹣（m+k2） +m2+k2
= 
，
令2m2﹣4m+1=2（m2﹣2），解得m= 
．
因此在x轴上存在定点M（ ，0），使得 为定值 
【解析】（I）求出圆x2+y2=a2/span>的圆心（0，0）到直线x﹣y﹣ 
=0的距离d，利用2=2 
，解得a2，又 
= 
，a2=b2+c2，联立解出即可得出．（II）假设在x轴上存在定点M（m，0），使得 
为定值．设A（x1，y1），B（x2，y2），直线方程与椭圆方程联立化为：（1+2k2）x2﹣4k2x+2k2﹣2=0，
利用根与系数的关系及其数量积运算性质可得 = 
，令2m2﹣4m+1=2（m2﹣2），解得m即可得出．
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
即可以解答此题．
