题目内容
在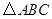 中,内角
中,内角 对边的边长分别是
对边的边长分别是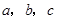 ,已知
,已知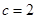 ,
,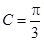 .
.
(1)若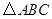 的面积等于
的面积等于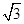 ,求
,求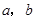 ;
;
(2)若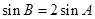 ,求
,求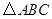 的面积.
的面积.
(1) ,
, .(2)
.(2) 。
。
解析试题分析:(1)由余弦定理得, ,又因为
,又因为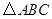 的面积等于
的面积等于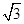 ,所以
,所以 ,得
,得 .联立方程组
.联立方程组
解得 ,
, . 7分
. 7分
(2)由正弦定理,已知条件化为 ,联立方程组
,联立方程组
解得 ,
, .
.
所以 的面积
的面积 . 14分
. 14分
考点:余弦定理;正弦定理;三角形的面积公式。
点评:本题主要考查三角函数正弦定理和余弦定理的灵活应用以及三角形的面积公式。三角函数正弦定理和余弦定理的灵活应用以及三角形的面积公式是考试中常考的内容,我们一定要熟练掌握。

练习册系列答案
相关题目
 中,角
中,角 所对应的边分别为
所对应的边分别为 ,
, 为锐角且
为锐角且 ,
, ,
, .
. 的值;
的值; ,求
,求 ABC中内角A,B,C的对边分别为a,b,c,已知2a=
ABC中内角A,B,C的对边分别为a,b,c,已知2a= c,
c, .
. 的值;
的值; ,求BD长。
,求BD长。 是角
是角 所对的边,且
所对的边,且 .
. 的大小;(2)若
的大小;(2)若 ,求△ABC周长的最大值。
,求△ABC周长的最大值。 ;
; 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是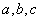 ,
,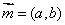 ,
, 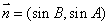 ,
, 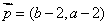
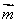 ∥
∥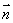 ,求证:
,求证: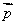 ,边长
,边长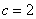 ,
,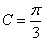 ,求
,求
 ,函数
,函数
 的最小正周期;
的最小正周期; 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边, ,且
,且 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。 +cos A=0.
+cos A=0. ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
 ;
;