题目内容
已知△ABC是椭圆
+
=1的内接三角形,F是椭圆的右焦点,且△ABC的重心在原点0,则A、B、C三点到F的距离之和为( )
| x2 |
| 25 |
| y2 |
| 9 |
| A.9 | B.15 | C.12 | D.8 |
设A(x1,y1),B(x2,y2),C(x3,y3),椭圆的离心率为e,
则|AF|=a-ex1,|BF|=a-ex2,|CF|=a-ex3,
所以|AF|+|BF|+|CF|=3a-e(x1+x2+x3),
因为△ABC的重心在原点O,∴x1+x2+x3=0,
又a=5,
∴|AF|+|BF|+|CF|=15.
故选B.
则|AF|=a-ex1,|BF|=a-ex2,|CF|=a-ex3,
所以|AF|+|BF|+|CF|=3a-e(x1+x2+x3),
因为△ABC的重心在原点O,∴x1+x2+x3=0,
又a=5,
∴|AF|+|BF|+|CF|=15.
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点.
的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点.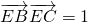 ,求△ABC外接圆的方程.
,求△ABC外接圆的方程. 的右焦点,过点E(2,0)且斜率为k的直线l与D交于A、B两点,C是点A关于x轴的对称点。
的右焦点,过点E(2,0)且斜率为k的直线l与D交于A、B两点,C是点A关于x轴的对称点。 ,求△ABC外接圆的方程。
,求△ABC外接圆的方程。 的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点。
的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点。 ,求△ABC外接圆的方程。
,求△ABC外接圆的方程。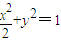 的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点.
的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点. ,求△ABC外接圆的方程.
,求△ABC外接圆的方程.