题目内容
已知F是椭圆D: 的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点.
的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点.
(Ⅰ)证明:点F在直线BC上;
(Ⅱ)若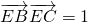 ,求△ABC外接圆的方程.
,求△ABC外接圆的方程.
(Ⅰ)证明:设直线l:y=k(x-2),A(x1,y1),B(x2,y2),C(x1,-y1),F(1,0),
由 得(2k2+1)x2-8k2x+8k2-2=0.
得(2k2+1)x2-8k2x+8k2-2=0.
所以 ,
,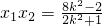 .
.
又△=64k4-8(2k2+1)(4k2-1)>0,则 .
.
而 ,
, ,
,
所以(x1-1)(kx2-2k)-(x2-1)(-kx1+2k)=k[2x1x2-3(x1+x2)+4= =0.
=0.
∴B、F、C三点共线,即点F在直线BC上.
(Ⅱ)解:因为 ,
, ,
,
所以 =(1-k2)[x1x2-2(x1+x2)+4]=
=(1-k2)[x1x2-2(x1+x2)+4]= =
= =1,
=1,
又k>0,解得 ,满足
,满足 .
.
代入(2k2+1)x2-8k2x+8k2-2=0,知 x1,x2是方程3x2-4x=0的两根,
根据对称性不妨设x1=0, ,即A(0,-1),C(0,1),
,即A(0,-1),C(0,1), .
.
设△ABC外接圆的方程为(x-a)2+y2=a2+1,把 代入方程得
代入方程得 ,
,
即△ABC外接圆的方程为 .
.
分析:(Ⅰ)设出直线l的方程,代入椭圆方程,利用向量共线,证明B、F、C三点共线,即点F在直线BC上;
(Ⅱ)利用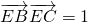 ,确定直线的斜率,从而可求A,B,C的坐标,即可求△ABC外接圆的方程.
,确定直线的斜率,从而可求A,B,C的坐标,即可求△ABC外接圆的方程.
点评:本题考查直线与椭圆的位置关系,考查向量知识的运用,考查圆的方程,考查学生的计算能力,属于中档题.
由
 得(2k2+1)x2-8k2x+8k2-2=0.
得(2k2+1)x2-8k2x+8k2-2=0.所以
 ,
,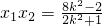 .
.又△=64k4-8(2k2+1)(4k2-1)>0,则
 .
.而
 ,
, ,
,所以(x1-1)(kx2-2k)-(x2-1)(-kx1+2k)=k[2x1x2-3(x1+x2)+4=
 =0.
=0.∴B、F、C三点共线,即点F在直线BC上.
(Ⅱ)解:因为
 ,
, ,
,所以
 =(1-k2)[x1x2-2(x1+x2)+4]=
=(1-k2)[x1x2-2(x1+x2)+4]= =
= =1,
=1,又k>0,解得
 ,满足
,满足 .
.代入(2k2+1)x2-8k2x+8k2-2=0,知 x1,x2是方程3x2-4x=0的两根,
根据对称性不妨设x1=0,
 ,即A(0,-1),C(0,1),
,即A(0,-1),C(0,1), .
.设△ABC外接圆的方程为(x-a)2+y2=a2+1,把
 代入方程得
代入方程得 ,
,即△ABC外接圆的方程为
 .
.分析:(Ⅰ)设出直线l的方程,代入椭圆方程,利用向量共线,证明B、F、C三点共线,即点F在直线BC上;
(Ⅱ)利用
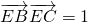 ,确定直线的斜率,从而可求A,B,C的坐标,即可求△ABC外接圆的方程.
,确定直线的斜率,从而可求A,B,C的坐标,即可求△ABC外接圆的方程.点评:本题考查直线与椭圆的位置关系,考查向量知识的运用,考查圆的方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 的右焦点,过点E(2,0)且斜率为k的直线l与D交于A、B两点,C是点A关于x轴的对称点。
的右焦点,过点E(2,0)且斜率为k的直线l与D交于A、B两点,C是点A关于x轴的对称点。 ,求△ABC外接圆的方程。
,求△ABC外接圆的方程。 的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点。
的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点。 ,求△ABC外接圆的方程。
,求△ABC外接圆的方程。 的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点.
的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点. ,求△ABC外接圆的方程.
,求△ABC外接圆的方程.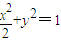 的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点.
的右焦点,过点E(2,0)且斜率为正数的直线l与D交于A、B两点,C是点A关于x轴的对称点. ,求△ABC外接圆的方程.
,求△ABC外接圆的方程.