题目内容

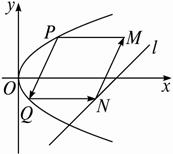
抛物线x2=4y的焦点为F，过点(0，-1)作直线l交抛物线A、B两点，再以AF、BF为邻边作平行四边形FABR，试求动点R的轨迹方程.

x2=4(y+3)(｜x｜＞4)


解析:

设R(x,y),∵F(0,1),∴平行四边形FARB的中心为C(,),l:y=kx-1,代入抛物线方程，得x2-4kx+4=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=4，且

△=16k2-16＞0，即|k|＞1    ①，

∴y1+y2===4k2-2,∵C为AB的中点.

∴消去k得x2=4(y+3),由①得，｜x｜＞4，

故动点R的轨迹方程为x2=4(y+3)(｜x｜＞4).

练习册系列答案
相关题目

抛物线有光学性质: 由其焦点射出的光线经抛物线折射后，沿平行于抛物线对称轴的方向射出，今有抛物线y2=2px(p＞0)  一光源在点M(,4)处，由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P，折射后又射向抛物线上的点Q，再折射后，又沿平行于抛物线的轴的方向射出，途中遇到直线l: 2x－4y－17=0上的点N，再折射后又射回点M(如下图所示)

 (1)设P、Q两点坐标分别为(x1,y1)、(x2,y2)，证明：y1·y2=－p2；

(2)求抛物线的方程；

(3)试判断在抛物线上是否存在一点，使该点与点M关于PN所在的直线对称？若存在，请求出此点的坐标；若不存在，请说明理由.

抛物线有光学性质：由其焦点射出的光线经抛物线折射后，沿平行于抛物线对称轴的方向射出，今有抛物线y2=2px(p＞0).一光源在点M(,4)处，由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P，折射后又射向抛物线上的点Q，再折射后，又沿平行于抛物线的轴的方向射出，途中遇到直线l：2x-4y-17=0上的点N，再折射后又射回点M(如图所示).

（1）设P、Q两点坐标分别为(x1,y1)、(x2,y2)，证明y1·y2=-p2；

（2）求抛物线的方程；

（3）试判断在抛物线上是否存在一点，使该点与点M关于PN所在的直线对称？若存在，请求出此点的坐标；若不存在，请说明理由.

抛物线有光学性质：由其焦点射出的光线经抛物线折射后，沿平行于抛物线对称轴的方向射出.今有抛物线y2=2px（p＞0）,一光源在点M（，4）处，由其发出的光线沿平行于抛物线对称轴的方向射向抛物线上的点P，折射后又射向抛物线上的点Q，再折射后，又沿平行于抛物线对称轴的方向射出，途中遇到直线l:2x-4y-17=0上的点N，再折射后又射回点M（如图所示）.

(1)设P、Q两点的坐标分别为(x1,y1),(x2,y2)，证明：y1y2=-p2;

(2)求抛物线的方程；

（3）试判断在抛物线上是否存在一点，使该点与点M关于PN所在的直线对称？若存在，请求出此点的坐标；若不存在，请说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网