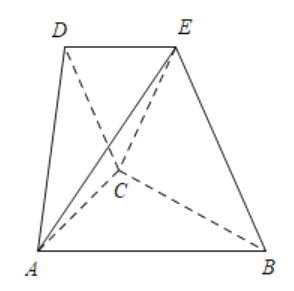
题目内容
【题目】如图,己知圆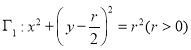 和双曲线
和双曲线![]() ,记
,记![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴负半轴的公共点分别为
轴负半轴的公共点分别为![]() 、
、![]() ,又记
,又记![]() 与
与![]() 在第一、第四象限的公共点分别为
在第一、第四象限的公共点分别为![]() 、
、![]() .
.

(1)若![]() ,且
,且![]() 恰为
恰为![]() 的左焦点,求
的左焦点,求![]() 的两条渐近线的方程;
的两条渐近线的方程;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)若![]() 恰为
恰为![]() 的左焦点,求证:在
的左焦点,求证:在![]() 轴上不存在这样的点
轴上不存在这样的点![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由圆的方程求出![]() 点坐标,得双曲线的
点坐标,得双曲线的![]() ,再计算出
,再计算出![]() 后可得渐近线方程;
后可得渐近线方程;
(2)设![]() ,由圆方程与双曲线方程联立,消去
,由圆方程与双曲线方程联立,消去![]() 后整理,可得
后整理,可得![]() ,
,
![]() ,由
,由![]() 先求出
先求出![]() ,回代后求得
,回代后求得![]() 坐标,计算
坐标,计算![]() ;
;
(3)由已知得![]() ,设
,设![]() ,由圆方程与双曲线方程联立,消去
,由圆方程与双曲线方程联立,消去![]() 后整理,可解得
后整理,可解得![]() ,
,![]() ,求出
,求出![]() ,从而可得
,从而可得![]() ,由
,由![]() ,可知满足要求的
,可知满足要求的![]() 点不存在.
点不存在.
(1)由题意圆方程为![]() ,令
,令![]() 得
得![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() ,
,![]() ,∴渐近线方程为
,∴渐近线方程为![]() .
.
(2)由(1)圆方程为![]() ,
,![]() ,
,
设![]() ,由
,由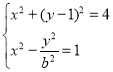 得,
得,![]() (*),
(*),
![]() ,
,![]() ,
,
![]()
![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
方程(*)为![]() ,即
,即![]() ,
,![]() ,代入双曲线方程得
,代入双曲线方程得![]() ,∵
,∵![]() 在第一、四象限,∴
在第一、四象限,∴![]() ,
,![]() ,
,
∴![]() .
.
(3)由题意![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]()
由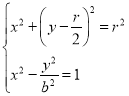 得:
得:![]() ,
,![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,
,![]() ,
,
![]() ,
,
所以![]()
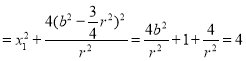 ,
,
![]() ,
,
![]() ,当且仅当
,当且仅当![]() 三点共线时,等号成立,
三点共线时,等号成立,
∴![]() 轴上不存在点
轴上不存在点![]() ,使得
,使得![]() .
.

【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: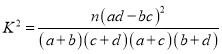 ,其中
,其中![]() )
)