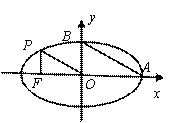
题目内容
(理)已知点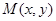 是平面直角坐标系上的一个动点,点
是平面直角坐标系上的一个动点,点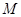 到直线
到直线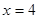 的距离等于点
的距离等于点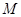 到点
到点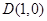 的距离的2倍.记动点
的距离的2倍.记动点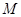 的轨迹为曲线
的轨迹为曲线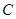 .
.
(1)求曲线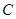 的方程;
的方程;
(2)斜率为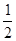 的直线
的直线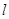 与曲线
与曲线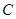 交于
交于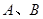 两个不同点,若直线
两个不同点,若直线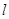 不过点
不过点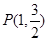 ,设直线
,设直线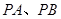 的斜率分别为
的斜率分别为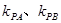 ,求
,求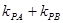 的数值;
的数值;
(3)试问:是否存在一个定圆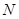 ,与以动点
,与以动点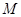 为圆心,以
为圆心,以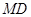 为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
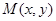 是平面直角坐标系上的一个动点,点
是平面直角坐标系上的一个动点,点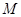 到直线
到直线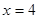 的距离等于点
的距离等于点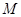 到点
到点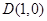 的距离的2倍.记动点
的距离的2倍.记动点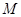 的轨迹为曲线
的轨迹为曲线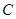 .
.(1)求曲线
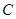 的方程;
的方程;(2)斜率为
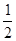 的直线
的直线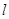 与曲线
与曲线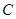 交于
交于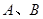 两个不同点,若直线
两个不同点,若直线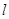 不过点
不过点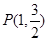 ,设直线
,设直线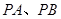 的斜率分别为
的斜率分别为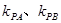 ,求
,求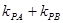 的数值;
的数值;(3)试问:是否存在一个定圆
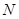 ,与以动点
,与以动点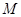 为圆心,以
为圆心,以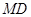 为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.(1) ;(2)0;(3)存在,定圆
;(2)0;(3)存在,定圆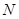 的方程为:
的方程为: .
.
 ;(2)0;(3)存在,定圆
;(2)0;(3)存在,定圆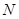 的方程为:
的方程为: .
.试题分析:(1)本题是求方程问题,由于没有告诉我们是什么曲线,因此我们可根据已知条件采取直接法求方程,由已知可得
 ,然后化简即可;(2)这是直线与圆锥曲线相交问题,解题方法是设直线
,然后化简即可;(2)这是直线与圆锥曲线相交问题,解题方法是设直线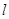 方程为
方程为 (注意
(注意 ,知道为什么吗?),与曲线方程联立方程组,并消去
,知道为什么吗?),与曲线方程联立方程组,并消去 得到关于
得到关于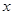 的二次方程,如果设
的二次方程,如果设 ,则可得
,则可得 (用
(用 表示),而
表示),而

 变形后表示成
变形后表示成 的式子,再把刚才的表达式代入计算应该就能得到结论;(3)假设存在这个定圆
的式子,再把刚才的表达式代入计算应该就能得到结论;(3)假设存在这个定圆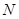 与动圆
与动圆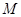 内切,则圆心距
内切,则圆心距 为两圆半径之差,从而
为两圆半径之差,从而 与两圆中的某个圆的半径之和或差为定值(定圆
与两圆中的某个圆的半径之和或差为定值(定圆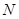 的半径),由于点
的半径),由于点 是椭圆的右焦点,这时联想椭圆的定义,若
是椭圆的右焦点,这时联想椭圆的定义,若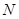 是椭圆的左焦点,则就有
是椭圆的左焦点,则就有 是常数,故定圆是以
是常数,故定圆是以 为圆心,4为半径的圆.
为圆心,4为半径的圆.试题解析:(1)由题知,有
 .
.化简,得曲线
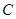 的方程:
的方程: .
.(2)∵直线
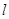 的斜率为
的斜率为 ,且不过
,且不过 点,
点,∴可设直线
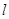 :
: .
.联立方程组
 得
得 .
.又交点为
 ,
,∴
 .
.∴



(3)答:一定存在满足题意的定圆
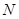 .
.理由:∵动圆
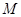 与定圆
与定圆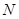 相内切,
相内切,∴两圆的圆心之间距离
 与其中一个圆的半径之和或差必为定值.
与其中一个圆的半径之和或差必为定值.又
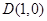 恰好是曲线(椭圆)
恰好是曲线(椭圆)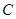 的右焦点,且
的右焦点,且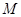 是曲线
是曲线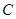 上的动点,
上的动点,记曲线
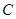 的左焦点为
的左焦点为 ,联想椭圆轨迹定义,有
,联想椭圆轨迹定义,有 ,
,∴若定圆的圆心
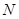 与点
与点 重合,定圆的半径为4时,则定圆
重合,定圆的半径为4时,则定圆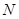 满足题意.
满足题意.∴定圆
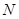 的方程为:
的方程为: .
.
练习册系列答案
相关题目
 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 的值.
的值. 交椭圆
交椭圆 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆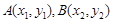 是椭圆
是椭圆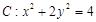 上两点,点
上两点,点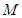 的坐标为
的坐标为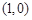 .
.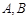 关于点
关于点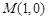 对称时,求证:
对称时,求证: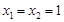 ;
;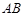 经过点
经过点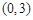 时,求证:
时,求证: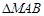 不可能为等边三角形.
不可能为等边三角形.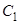 :
: 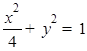 与双曲线
与双曲线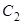 的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )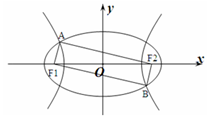
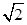 B.
B.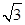 C.
C.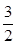 D.
D.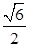
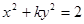 表示焦点在
表示焦点在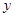 轴上的椭圆,那么实数
轴上的椭圆,那么实数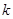 的取值范围是( )
的取值范围是( )



 、
、 分别是椭圆
分别是椭圆 的左、右焦点,点
的左、右焦点,点 在椭圆
在椭圆 上,线段
上,线段 的中点在
的中点在 轴上,若
轴上,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



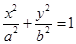
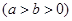 的焦点垂直于
的焦点垂直于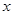 轴的弦长为
轴的弦长为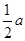 ,则双曲线
,则双曲线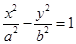 的离心率
的离心率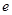 的值是( )
的值是( )


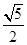
 =1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=
=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
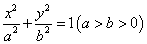 的左焦点,P是椭圆上一点,PF⊥x轴,OP∥AB(O为坐标原点),则该椭圆的离心率是( )
的左焦点,P是椭圆上一点,PF⊥x轴,OP∥AB(O为坐标原点),则该椭圆的离心率是( )