题目内容
设P为双曲线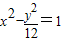 上的一点,F1,F2是该双曲线的两个焦点,若
上的一点,F1,F2是该双曲线的两个焦点,若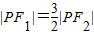 ,则cos∠F1PF2为 .
,则cos∠F1PF2为 .
【答案】分析:解决焦点三角形问题一般要用到两种知识,一是曲线定义,本题中由双曲线定义可得焦半径之差,已知有焦半径之比,故可求出焦半径或其关系;二是余弦定理,利用解三角形知识求角的余弦值.
解答:解:由 得a2=1,b2=12,c2=13,
得a2=1,b2=12,c2=13,
设|PF1|=3d,|PF2|=2d,则|3d-2d|=2,d=2
在△F1PF2中,由余弦定理得,cos∠F1PF2= =
= =-
=- .
.
故答案为:- .
.
点评:本题考查了双曲线的标准方程及其定义,双曲线的焦点三角形中的计算,余弦定理的运用.
解答:解:由
 得a2=1,b2=12,c2=13,
得a2=1,b2=12,c2=13,设|PF1|=3d,|PF2|=2d,则|3d-2d|=2,d=2
在△F1PF2中,由余弦定理得,cos∠F1PF2=
 =
= =-
=- .
.故答案为:-
 .
.点评:本题考查了双曲线的标准方程及其定义,双曲线的焦点三角形中的计算,余弦定理的运用.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 上的一点,F1、F2是该双曲线的两个焦点,若
上的一点,F1、F2是该双曲线的两个焦点,若 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( ) B.12 C.12
B.12 C.12 D.24
D.24 上的一点,F1、F2是该双曲线的两个焦点,若
上的一点,F1、F2是该双曲线的两个焦点,若 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( ) B.12 C.12
B.12 C.12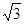 D.24
D.24 上的一点且位于第一象限。若
上的一点且位于第一象限。若 、
、 为此双曲线的两个焦点,且
为此双曲线的两个焦点,且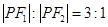 ,则
,则 的周长为 ( )
的周长为 ( ) 上的一点,
上的一点, 是该双曲线的两个焦点,若
是该双曲线的两个焦点,若 ,则
,则 的面积为___________.
的面积为___________.