题目内容
已知曲线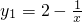 与
与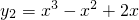 在x=x0处切线的斜率的乘积为3,则x0的值为
在x=x0处切线的斜率的乘积为3,则x0的值为
- A.-2
- B.2
- C.

- D.1
D
分析:对曲线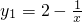 与
与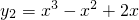 进行求导,把x=x0代入,根据已知条件进行求解;
进行求导,把x=x0代入,根据已知条件进行求解;
解答:∵曲线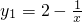 与
与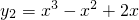
∴y′1= 与
与 =3x2-2x+2,
=3x2-2x+2,
∵曲线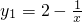 与
与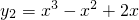 在x=x0处切线的斜率的乘积为3,
在x=x0处切线的斜率的乘积为3,
∴ ×(3x02-2x0+2)=3,
×(3x02-2x0+2)=3,
解得x0=1,
故选D.
点评:此题主要考查导数的几何意义及其求导问题,要知道导数与斜率的关系,此题是一道基础题.
分析:对曲线
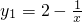 与
与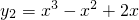 进行求导,把x=x0代入,根据已知条件进行求解;
进行求导,把x=x0代入,根据已知条件进行求解;解答:∵曲线
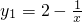 与
与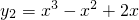
∴y′1=
 与
与 =3x2-2x+2,
=3x2-2x+2,∵曲线
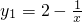 与
与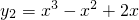 在x=x0处切线的斜率的乘积为3,
在x=x0处切线的斜率的乘积为3,∴
 ×(3x02-2x0+2)=3,
×(3x02-2x0+2)=3,解得x0=1,
故选D.
点评:此题主要考查导数的几何意义及其求导问题,要知道导数与斜率的关系,此题是一道基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 f′(x0)+alnx0≤ax0成立(其中f′(x)为函数f(x)的导函数),求实数a的取值范围.
f′(x0)+alnx0≤ax0成立(其中f′(x)为函数f(x)的导函数),求实数a的取值范围.