题目内容
已知椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
(1)求椭圆C的方程;
(2)已知A为椭圆C的左顶点,直线l过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率k1,k2满足k1+k2=m(定值m≠0),求直线l的斜率.
解:(1)∵椭圆离心率为 ,
,
∴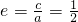 ,∴
,∴ (2分)
(2分)
又椭圆经过点 ,∴
,∴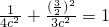
解得c=1,∴ (3分)
(3分)
∴椭圆C的方程是 …(4分)
…(4分)
(2)若直线l斜率不存在,显然k1+k2=0不合题意 …(5分)
设直线方程为l:y=k(x-1),M(x1,y1),N(x2,y2)
联立方程组 得(3+4k2)x2-8k2x+4k2-12=0…(7分)
得(3+4k2)x2-8k2x+4k2-12=0…(7分)
∴ …(8分)
…(8分)
∴k1+k2=
 =
= =
=
= =k(
=k( )=-
)=-
∵k1+k2=m,∴- =m,
=m,
∴k= .
.
分析:(1)利用椭圆的离心率为 ,且经过点
,且经过点 ,可求几何量,从而可得椭圆的方程;
,可求几何量,从而可得椭圆的方程;
(2)设出直线方程与椭圆方程联立,利用韦达定理及k1+k2=m(定值m≠0),即可求直线l的斜率.
点评:本题考查椭圆的几何性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,正确运用韦达定理是关键.
 ,
,∴
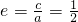 ,∴
,∴ (2分)
(2分)又椭圆经过点
 ,∴
,∴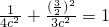
解得c=1,∴
 (3分)
(3分)∴椭圆C的方程是
 …(4分)
…(4分)(2)若直线l斜率不存在,显然k1+k2=0不合题意 …(5分)
设直线方程为l:y=k(x-1),M(x1,y1),N(x2,y2)
联立方程组
 得(3+4k2)x2-8k2x+4k2-12=0…(7分)
得(3+4k2)x2-8k2x+4k2-12=0…(7分)∴
 …(8分)
…(8分)∴k1+k2=

 =
= =
=
=
 =k(
=k( )=-
)=-
∵k1+k2=m,∴-
 =m,
=m,∴k=
 .
.分析:(1)利用椭圆的离心率为
 ,且经过点
,且经过点 ,可求几何量,从而可得椭圆的方程;
,可求几何量,从而可得椭圆的方程;(2)设出直线方程与椭圆方程联立,利用韦达定理及k1+k2=m(定值m≠0),即可求直线l的斜率.
点评:本题考查椭圆的几何性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,正确运用韦达定理是关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: