题目内容
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 9 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)该小组发现种子的发芽数![]() (颗)与昼夜温差
(颗)与昼夜温差![]() (℃)呈线性相关关系,试求:线性回归方程
(℃)呈线性相关关系,试求:线性回归方程![]() .
.
(参考公式:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
,![]() .其中
.其中![]() ,
,![]() 表示样本均值.
表示样本均值.
参考数据:![]() ;
;![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意,用列举法求古典概型的概率即可;
(2)根据参考数据,结合题意,即可求得回归直线方程.
(1)用数对![]() 表示基本事件:
表示基本事件:
则基本事件有如下10个:
![]()
满足题意的有如下3个:
![]()
故满足题意的概率为![]() .
.
(2)由题可知:![]()
![]() ,
,
![]()
![]() .
.
故可得
![]() ,
,
![]()
![]() .
.
故所求回归直线方程为![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
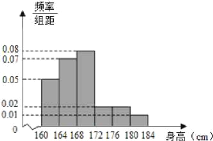
【题目】为了了解学生的学习情况,一次测试中,科任老师从本班中抽取了n个学生的成绩(满分100分,且抽取的学生成绩均在![]() 内)进行统计分析.按照
内)进行统计分析.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图和频数分布表.
的分组作出频率分布直方图和频数分布表.

频数分布表 | |
| x |
| 4 |
| 10 |
| 12 |
| 8 |
| 4 |
(1)求n,a,x的值;
(2)在选取的样本中,从低于60分的学生中随机抽取两名学生,试问这两名学生在同一组的概率是多少?
【题目】为调查乘客的候车情况,公交公司在某为台的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,将他们的候车时间(单位:分钟)作为样本分成
人,将他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 候车时间 | 人数 |
一 |
|
|
二 |
|
|
三 |
|
|
四 |
|
|
五 |
|
|
(1)求这![]() 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这![]() 名候车乘客中候车时间少于
名候车乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的![]() 人中随机抽取
人中随机抽取![]() 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.